 |
 |
 |
|
|
||
. |
 Cadena Cadena
|
 Lenguajes Lenguajes
|
 Gramáticas Gramáticas. |
 Produccion Produccion
|
 Diagrama Diagrama
|
 Traducción Traducción. |
 Canónico Canónico
|
 Ambiguedad Ambiguedad
|
 Arboles Arboles. |
 Automatas Automatas
|
 Compiladores Compiladores
|
- SEMIÓTICA O SEMIOLOGÍA
Ciencia de SIGNOS - GRAMÁTICA:
- SINTAXIS:
- SEMANTICA:
- MORFOLOGIA:
- RAICES:
Como la española –duc, que da lugar a producir, reducir, deducir. - DESINENCIAS:
De género, número, conjugación, tiempo verbal. - PREFIJOS:
Se añaden a la raíz para crear palabras compuestas
- (pro-, intro-, con-, re-) - SUFIJOS:
Derivativos para formar
- Aumentativos (como -ón, -azo),
- Diminutivos (como -ito, -ico), - ADJETIVOS:
Como -tivo, y adverbios como -mente. - ALTERACIONES FONETICAS:
De formas de verbos irregulares
- como: poder, puedo, pude. - FONETICA:
Lingüística estructural:
- Significante: Forma del signo
- Significado: Lo que representa
Define estructuras Gramáticales
- Lenguaje natural o artificial.
- Combinación de símbolos.
- Generación del lenguaje formal.
- Sentencias formadoras.
Chomsky propone:
a) Una Gramática universal como:
Competencia lingüística del conocimiento innato humano con:
- Lenguaje prefigurado genéticamente
- Módulos cerebrales especializados.
- Gen cerebral de función lenguaje.
b) Reglas de gestión de Gramáticas:
- Universales.
- Específicas de cada lengua.
Operando "transformaciones", de unidades subyacentes.
La Gramática es:
a) TRANSFORMACIONAL:
Si genera oraciones "reconocibles"
b) GENERATIVA:
Si genera oraciones "aceptables"
Sintagma:.
Unidad sintáctica (Palabra/grupo de cadenas) con una función respecto a otras.
Reglas para hablar y escribir
- Relaciones de palabras en la oración:
- Elementos para formar una oración,
- Reglas para formar la oración.
- Oraciones coherentes,
En lenguajes artificiales las oraciones coherentes se forman con:
- "palabras formales", o
- "palabras reservadas" o
- "comandos reconocibles".
Lexemas: Significado de palabras.
- Signos lingüísticos.
- Palabras y oraciones.
Vocabulario:
- Palabras o unidades, formadas por rasgos semánticos.
Morfemas: Formato de palabras.
Unidades portadoras de significación, tales como:
Fonemas: Sonidos de la lengua,
Abarca: Sonidos
- Unidades mínimas de significación.
- Elementos fónicos: suprasegmentales (entonación).
Paradigma:
Manejar el silencio
es más difícil
que manejar la palabra
Georges Clemenceau




A L F A B E T O Si A es un alfabeto y a ∈ A, implica que a es un símbolo de A. Si B es un alfabeto y ∪, ∩, ℷ, ∈ ∈ B implica que ∪, ∩, ℷ, ∈ son símbolos de B. Así, para el alfabeto A = { a, b, . . . , y, z } arroz y zorra serán palabras. Sus parámetros son: |
- LONGITUD:
Cantidad de caracteres
que compone la cadena
Si w es cadena sobre un alfabeto A,
su longitud se representa
como |w|
Ejemplo: :
Para la cadena
w = “zorra”
perteneciente al alfabeto
A = { a, b, . . . , y, z },
tendrá como
longitud |w| = 4 - PALABRA VACIA ℷ :
Cadena cuya longitud es:
| ℷ | = 0,
luego, carece de todo símbolo. - UNIVERSO DEL ALFABETO: W (A):
Formado por palabras generadas con los símbolos del alfabeto AEjemplo:
Para el alfabeto
A = { a, b, . . . , y, z }
W (A) = { ℷ, arroz, zorra, . . } - SUBCADENA:
La cadena w
es subcadena o subpalabra
de la cadena p,
si existe p = u w z.Ejemplo:
w = color
es subcadena de
p = des color ear- PREFIJO:
De una cadena es cualquier subcadena del comienzo de esa cadena.
Ejemplo:
La cadena abc tiene: ℷ, a, ab, abc como prefijos. - SUFIJO:
De una cadena es una subcadena del final de esa cadena.
Ejemplo:
La cadena abc tiene: ℷ, c, bc, abc como sufijos.
- PREFIJO:
- IGUALDAD:
Dos cadenas son iguales si tienen la misma longitud, símbolos y posición.
|
Operaciones |
- CONCATENACION:
Si w y z son dos cadenas,
su concatenación w.z
será otra cadena formada por símbolos de w
seguidos por los símbolos de z.Ejemplo:
Si la cadena
w = “tecno”
se concatena o yuxtapone
con la cadena z = “lógico”,
Genera otra cadena
wz o w.z = “tecnológico”,
de longitud: |w.z| = |w| + |z|.La concatenación de w con la cadena vacía ℷ
generará w. ℷ = “tecno”. - POTENCIA:
Para la cadena w del alfabeto A,
su potencia enésima
se forma por concatenación n veces de w
Expresada como:
wn = w . w . w . . . w.
( n factores w )Ejemplo:
Para la cadena w = 12
sobre el alfabeto A = {1, 2}
se generan las potencias:w0 = ℷ,
w1 = 12,
w2 = 1212,
w3 = 121212 - INVERSA:
o REFLEXION o TRANSPUESTA
o REVERSO,
Imagen refleja de la cadena. Ejemplo:Para la cadena: La Inversa es: w = roma w(I) = amor; z = arroz z(I) = zorra x = oir x(I) = rio
- PALINDROMO:
Cadena con la misma imagen especular.
Ejemplo:
n e u q u e n, r a d a r - RELACION THUE:
Simbolizada como
W( ->T) Z,
Representa en un alfabeto A
la relación entre sus cadenas W y Z
que permite generar nuevas palabras,
por procedimiento de sustitución.Así, sean:
W y Z
dos palabras del alfabeto A
A una palabra del lenguaje A*La relación de Thue o thueica
W ( ->T) Z,
representa la correspondencia
entre la palabra A
con otra palabra B,
que se obtiene por sustitución de W por Z.


Conjuntos de sonidos, señales, símbolos, caracteres de un lenguaje Pueden ser:
|
|||||||||||||||
|
Libre del Contexto
Con producciones: | A ÎSN, v ÎST+ } |
Sin restricciones
Con producciones: P = { ( u::= v) | u = x Ay, u Î A+, v, x, y ∈ A ∈ AN } |
||||||||||||||
|
Dependiente del Contexto
Consideran lo anterior y posterior del símbolo que se sustituye. P = { (S ::= ℷ) o ( xAy::=xvy )
La palabra generada tiene longitud mayor o igual que la anterior de la derivación. "x" e "y" son el contexto de transformación de A en v. Las derechas e izquierdas de los lenguajes, tienen una parte en común Admite la regla compresora S ::= ℷ. |
Regular
Las Producciones limitan a un solo Símbolo Terminal en la izquierda. En la dereccha, puede o no, estar seguido de un solo Símbolo No terminal.
|
||||||||||||||
REPRESENTADO en formato de:
- EXTENSION:
Ej: Para el alfabeto A = {1},
Como: L = {1, 11, 111,..}
sus palabras son cadenas de longitudes finitas de unos. - COMPRENSION:
Como: L = { 1(n) }
para n = 1, 2, 3..}.
DESCRIBIRSE como LENGUAJE:
- FINITO:
Enumerando todas sus palabras componentes. - INFINITO:
Definiendo sus reglas o requerimientos sintácticos. - LENGUAJE VACIO ℷ:
Cuando no tiene ninguna cadena.
Para el alfabeto A:
- dados sus lenguajes L1 y L2,
- si todas las cadenas de L1 son también cadenas de L2,
- se dice que L1 es sublenguaje de L2
Ejemplo: Para los lenguajes
L1 = {zorra, arroz, amor, roma, oir, rio } y
L2 = {zorra, arroz, amor, roma, oir, rio tecno}
Se dice que L1 es sublenguaje de L2
CIERRE o CERRADURA:
O clausura. Simbolizada por la
Estrella de Kleene E*
Es el lenguaje compuesto por todas las cadenas sobre el alfabeto A, incluido ℷ;
por ello para cualquier alfabeto A * es infinito.
Ejemplo:
COMPLEMENTO de LENGUAJES:
A = {1}
A* = {L, 1, 11, 111,.....}.
Dados los lenguajes L1 y L2,
se dice que el lenguaje ~L2
es complemento del lenguaje L1
si y solo si
L1 = A* - L2 = { u ∈ A* - u Ï L1 }
Por ello será:
~A* = Lenguaje vacio
|
Lenguajes Abstractos: |
- UNIÓN DE LENGUAJES ∪ :
- INTERSECCIÓN de LENGUAJES: ∩
- RESTA DE LENGUAJES:
- PRODUCTO DE LENGUAJES:
- INVERSIÓN DE LENGUAJES:
- CONCATENACIÓN DE LENGUAJES:
- POTENCIA DE LENGUAJES:
- RECURSIVIDAD de LENGUAJES:
- Especificar algunos objetos primarios del conjunto.
- Diseñar reglas para generar más objetos del conjunto,
a partir de tales objetos primarios conocidos. - Plantear que solo los objetos construidos de este modo
pueden pertenecer al conjunto.
Para el alfabeto A,
sea w una cadena de los lenguajes L1 y L2,
la unión È: de L1 con L2
contendrá todas las palabras
que pertenezcan a cualquiera de los dos lenguajes;
Generan así un nuevo lenguaje
formado por todas las palabras sin repetición,
que pertenezcan alguno de estos lenguajes:
L = L1 È L2 = { w | w ∈ L1
con
w ∈ L2 }
Ejemplo: Para los lenguajes
L1 = { zorra, arroz, amor, roma, oir, rio } y
L2= { zorra, arroz, amor, roma, tecno }
L = L1 È L2 = { zorra, arroz, amor, roma, oir, rio, tecno }
Para el alfabeto A,
Sea w cadena de los lenguajes L1 y L2;
La intersección L1 intersección L2
Genera un nuevo lenguaje
formado por todas las palabras
que pertenezcan simultáneamente a los dos lenguajes:
L = L1 ∩ L2 = { w | w pertenece L1 ∩ w pertenece L2 }
Ejemplo: Para los lenguajes
L1={ zorra, arroz, amor, roma, oir, rio}
L2={ zorra, arroz, amor, roma, tecno }
L = L1 ∩ L2 = { zorra, arroz, amor, roma }
Para el alfabeto A,
sea w una cadena de los lenguajes L1 y L2
la resta L1 - L2,
genera un nuevo lenguaje
formado por todas las palabras
que pertenezcan a L1
y que no pertenezcan a L2
L = L1 - L2 =
L = { w | w ∈ L1 y w Ï L2 }
Ejemplo: Para los lenguajes
L1 = { zorra, arroz, amor, roma, oir, rio}
L2 = { zorra, arroz, amor, roma, tecno}
La resta:
L = L1 - L2 = { oir, rio }
El producto de los lenguajes L1 y L2
se representada como:
L1 . L2 = { uw | u ∈ L1 È w ∈ L2 },
Es el lenguaje generado
con cada palabra de L1
concatenada a su derecha
con cada palabra de L2.
Es el inverso del lenguaje L
Sean,
respectivamente w y x
cadenas de los lenguajes L1 y L2 del alfabeto A.
Su lenguaje de concatenación
L = L1 . L2
se generará por todas las palabras
que se pueden formar por concatenación
de una palabra de L1 y
otra palabra L2
de modo que:
L = L1 . L2 =
L = {w.x | w ∋ L1 y x ∋ L2 };
Ejemplo: Para los lenguajes
L1 = { pio } y
L2 = { joso, nono } ,
Lenguaje concatenado:
L = L1 . L2 = { piojoso, pionono }
Sea L1 un lenguaje del alfabeto A,
Su potencia enésima es la
la concatenación n veces del leguaje con si mismo
representada como
L1n = L1.L1.. .L1 ( n factores )
Ejemplo: Para el lenguaje
L1 = { pio }
se generan las potencias:
L1. L1 = {piopio},
L1. L1. L1 = {piopiopio}
La definición recursiva abarca un proceso de:
|
Cadenas ( X ::= Y ) ( x, y ), x, y ∈ A* De manera que si se encuentra x como parte de cualquier palabra v se puede sustituir x por y en v Así se transforma una cadena en otra. |
L ( A2 ) = { 0, 1 }
se generan las producciones
( 000 ::= 010 ) o
( 10 ::= 01 )

DERIVACION |
Es una forma de aplicación de la producción.
- DERIVACION DIRECTA:
( u --> w ) :
- DERIVACION: →
( u → w ) - DERIVACION mas a la IZQUIERDA:
- DERIVACION mas a la DERECHA:
Aplicación de una producción ( x ::= y ) a una palabra v para convertirla en otra palabra w, donde v = x.y.u, w = z.y.u
( v, w, z, u ∈ A* ). Se cumple que para cada producción ( x ::= y ) Hay derivación directa x a y: x -> y, Se deduce de lo anterior con hacer x = u = L.
Ejemplo:
Con las producciones:
P1 = ( 000 ::= 010 ) y
P2 = ( 10 ::= 01 )
y la palabra 1000,
se logran las derivaciones directas:
1000 (P1)--> 1010, 1010 (P2)--> 0110, 0110 (P2)--> 0101 y 0101 (P2)--> 0011
Aplicación de una sentencia de producciones a una palabra.
Ejemplo:
La ejecución continuada en el Ejemplo anterior,
proporciona una derivación de la palabra 1000 a la palabra 0011.
1000 (P1)--> 1010 (P2)--> 0110 (P2)--> 0101 (P2)--> 0011
Ocurre cuando se usa en cada derivación directa la producción aplicada a los símbolos más a la izquierda de la palabra.
La derivación más a la izquierda
Ejemplo anterior
será:
1000 (P2)--> 0100 (P2)--> 0010 (P2)--> 0001 (P1)--> 0101 (P2)--> 0011
Ocurre cuando se utiliza en cada derivación directa la producción aplicada
a los símbolos más a la derecha de la palabra.
Para el Ejemplo anterior:
1000 (P1)--> 1010 (P2)--> 1001 (P2)--> 0101 (P2)--> 0011
|
DIAGRAMA de SINTAXIS: Consiste en una imagen de las producciones para ver las sustituciones en forma dinámica, como movimientos a través del diagrama. |
Ejemplo:
Los diagramas siguientes resultan
de la traducción de conjuntos de producciones típicos, que son, las producciones que aparecen en el lado derecho de algún enunciado
BNF (forma Backus-Naur).
< w > ::= < w1 > < w2 > < w3 > < w > ::= < w1 > < w2 > | < w1 >a | bc< w2 > < w > ::= ab< w >. < w > ::= ab | ab< w >.
NOTACIÓN BNF
(forma Backus-Naur Form):
Describe la sintaxis, mediante un metalenguaje
que utiliza los metasímbolos:
< > ::= |
y define las reglas por medio de "producciones"
Ejemplo:
< digito > ::= 0|1|2|3|4|5|6|7|8|9
Esta notación es una alternativa br>para desplegar las producciones de las gramáticas de tipo 2 GIC, br>cuyos lados izquierdos son símbolos no terminales únicos.
Así, la gramática:
GIC = ( ST, SN, S, P )=
({ 0, 1 }, { A, B }, A, P )
genera el lenguaje:
L ={ 11, 101, 111 },
con las producciones:
P = { ( A ::= 1B1 ),
( A ::= 11),
( B ::= 1 ),
( B ::= 0 ) },
y las derivaciones:
A --> 11
A --> 1B1 --> 101
A --> 1B1 --> 111
Para cada símbolo w,
se combina todas las producciones que tienen a w como lado izquierdo.
El símbolo w permanece a la izquierda,
y los lados derechos asociados con w son enumerados juntos,
separados por el símbolo |.
El símbolo relacional
se reemplaza por el símbolo ::=.
Los símbolos no terminales,
serán encerrados entre paréntesis agudos < >.
Los símbolos no terminales pueden tener espacios dentro de ellos.
Así:
< palabra1 palabra2 >
Muestra que la cadena entre paréntesis debe considerarse como una "palabra", no como dos palabras.
Se puede utilizar el espacio como una "letra" conveniente y legítima en una palabra,
mientras se utilice los paréntesis agudos para delimitar las palabras.
Ejemplo:
En notación BNF,
ciertas producciones pueden tener
el siguiente formato:
< oración> ::= < sujeto> < predicado> < sujeto> ::= Juan | Julia < predicado> ::= < verbo> < adverbio> < verbo> ::= maneja | corre < adverbio> ::= descuidadamente | rápido | frecuentemente

PRODUCCION RECURSIVA |
aparece en una de las cadenas del lado derecho.
Ejemplo:
En la notación BNF, de ciertas producciones aparecerán:
< vo > ::= a< w > < w > ::= bb< w > | c
Como en el lado izquierdo de una producción aparecen también en una de las cadenas del lado derecho,
pues, < w > aparece a la izquierda, y aparece en la cadena bb < w >, la producción w bbw es recursiva.
Si una producción recursiva tiene a w como lado izquierdo,
la producción es normal si
w aparece sólo una vez en el lado derecho
y es el símbolo del extremo derecho.
En el lado derecho también pueden aparecer otros símbolos no terminales.
La producción recursiva w bbw es normal.
Ejemplo:
La notación BNF se utiliza para especificar los lenguajes de programación reales.
Ejemplo:
Un subconjunto de la gramática de PASCAL
que describe la sintaxis de los números decimales
se puede ver como una minigramática
cuyo lenguaje consta de números decimales.
Sea:
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, .} (ST)
N = {número-decimal, fracción-decimal, entero-sin-signo, dígito}.(SN)
V = S N (V es unión de S con el conjunto N )
G = ( ST, SN, A, P )
la gramática con conjuntos de símbolos V y S,
con el axioma o símbolo inicial A "número decimal"
y con las producciones P dadas en forma BNF
como sigue:
< número-decimal> ::= < entero-sin-signo> | < fracción-decimal> | < fracción-decimal> ::= < entero-sin-signo> < fracción-decimal> < entero-sin-signo> ::= < dígito> | < dígito> < entero-sin-signo> < dígito> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Muchas gramáticas diferentes pueden producir el mismo lenguaje.
Si se reemplaza la línea anterior número 3 con la línea: 3'.
< entero-sin-signo> ::= < dígito> | < entero-sin-signo> < dígito>
se tendría una gramática diferente que produce exactamente el mismo lenguaje,
Los números decimales formados de manera correcta.
Sin embargo, esta gramática contiene una producción recursiva que no es normal.
Ejemplo:
Una gramática especifica una parte de varios lenguajes de programación reales.
En estos lenguajes,
- Un identificador (un nombre para una variable, función, subrutina, etcétera)
- debe estar compuesto por letras y dígitos y debe comenzar con una letra.
La siguiente gramática, con las producciones dadas en BNF,
tiene estos identificadores como su lenguaje.
G = (V, S, identificador, )
N = {identificador, resto, dígito, letra}
S = {a, b, c, . . , z, 0, 1, 2, 3, . . , 9},
V = N U S
< identificador>::= < letra>| < letra>< resto> < resto>::= < letra>| < dígito>| < letra>< resto>| < dígito>< resto> < resto>::= a | b | c . . . | z < dígito>::= 0 | 1 | 2 | 3 | 4 | 5 | 6| 7 | 8 | 9
|
ESQUEMA de TRADUCCION: Un atributo queda caracterizado por un identificador o nombre y un tipo o clase. Se inserta acciones, código Perl/Python/C, en medio de las partes derechas. En ese código es posible referenciar los atributos de símbolos de la gramática como variables del lenguaje subyacente. El orden en que se evalúan los fragmentos de código
|
1 sub esquema_de_traduccion {
2 my $node = shift;
3
4 for my $child ($node->children) { # de izquierda a derecha
5 if ($child->isa('ACTION') {
6 $child->execute;
7 }
8 else { esquema_de_traduccion($child) }
9 }
10 }
El bucle de la línea 4
recorre a los hijos de izquierda a derecha,
se debe dar la siguiente condición
para que un esquema de traducción funcione:
Para cualquier regla de producción aumentada con acciones,
de la forma
A X1...Xj action{( $ A {b}, $ X1{c}...Xn{d})} Xj+1...Xn
Requiere que los atributos evaluados en la acción insertada
después de Xj dependan de atributos y variables
que fueron computadas durante la visita de los hermanos izquierdos o de sus ancestros.
En particular no deberían depender de atributos
asociados con las variables Xj+1 ...Xn.
No significa que no sea correcto evaluar
atributos de Xj+1 ...Xn en esa acción.
Así, un ESQUEMA DE TRADUCCIÓN
es la gramática independiente del contexto
en cuyas partes derechas de sus reglas de producción
se insertaron en las fragmentos de código
denominados ACCIONES SEMÁNTICAS,
que actúan, calculan y modifican
los atributos asociados con los nodos del árbol sintáctico.
El orden en que se evalúan los fragmentos
es el de un recorrido primero-profundo
del árbol de análisis sintáctico.
Para aplicar un esquema de traducción
hay que construir el árbol sintáctico y
después aplicar las acciones empotradas
en las reglas en el orden de recorrido primero-profundo.
Ejemplo:
A a {action}ß
Si en la regla
A a ß el nodo asociado con una producción:
deducimos un fragmento de código:
La acción {action}
se ejecutará después de todas las acciones asociadas con el recorrido del subárbol de a
y antes que todas las acciones asociadas con el recorrido del subárbol ß.
El siguiente esquema de traducción
recibe como entrada una expresión en infijo y
produce como salida su traducción a postfijo
para expresiones aritméticas con sólo restas de números:
expr expr1 - NUM { $expr{TRA} =
$expr[1]{TRA}." ".$NUM{VAL}." - "}
expr NUM{ $expr{TRA} = $NUM{VAL} }
Las apariciones de variables sintácticas en una regla de producción se indexan
Ejemplo, para distinguir de que nodo del árbol de análisis.
El atributo de un nodo usa una indexación tipo hash.
Aquí VAL es un atributo de los nodos de tipo NUM denotando su valor numérico y para accederlo escribiremos $NUM{VAL}.
Análogamente $expr{TRA} denota el atributo "traducción" de los nodos de tipo expr.
Un atributocuyo valor en un nodo es computado como atributos de los hijos del nodo (atributo sintetizado).
Ejemplo:
Atributo heredado es el tipo de las variables en las declaraciones:
decl type{ $list{T} = $type{T} } list
type INT { $type{T} = $int }
type STRING{ $type{T} = $string }
List ID, { $ID{T} = $list{T}; $list[1]{T} = $list{T} }list1
List ID { $ID{T} = $list{T} }
|
SISTEMAS CANONICOS: La inteligencia suele asociarse con "regularidades" y el comportamiento inteligente suele asociarse a ejecutar reglas. Newell y Simon
Así, se asemeja al proceso de memoria humano:
Las reglas de producción es un formalismo usado en teoría de autómatas, gramáticas formales y en el diseño de lenguajes de programación. |
A = {a,b,c} (alfabeto)
Axiomas: a, b, c, aa, bb, cc
Producciones
$ a$a
$ b$b
$ c$c
Estas reglas generan palíndromos.
Ejemplo: b a c a b.
Las reglas de producción de sistemas expertos difieren de las producciones.
Reglas de producción manipulan estructuras de símbolos, como listas o vectores.
Se tiene un conjunto de:
N de nombres de objetos en el dominio
P de propiedades de atributos de objetos
V de valores que los atributos pueden tener
Generalmente se usa una tripleta:
(objeto atributo valor).
A veces las reglas se ponen:
P1, . . .Pm
Q1, . . .Qn.
Que significa:
IF las condiciones P1 y P2 y . .y Pm
se cumplen
THEN realiza las acciones
Q1 y Q2 y . . y Qn.
Ejemplo:
IF Animal es_un carnivoro AND
Animal color cafe AND
Animal tiene rayas
THEN Animal es tigre
PROPIEDADES de las REGLAS:
- MODULARIDAD:
Cada reglas define un pequeño y relativamente idependiente pedazo de conocimiento - INCREMENTALIDAD:
Nuevas reglas pueden ser añadidas a la base de conocimiento relativamente independiente de las demás - MODIFICABILIDAD:
Como consecuencia de la modularidad, las reglas viejas pueden ser modificadas - TRANSPARENCIA:
Habilidad de explicar sus decisiones y soluciones
UN SISTEMA DE PRODUCCIÓN tiene:
- UN CONJUNTO DE REGLAS:
Base de conocimiento. - UN INTERPRETE DE REGLAS:
O máquina de inferencia, que decide que regla aplicar, controla la actividad del sistema. - UNA MEMORIA DE TRABAJO:
Que guarda los datos, metas, y resultados intermedios

EJEMPLOS LENGUAJE SIN RESRICCIONES |
Ejemplo 1:
La gramática G = ( S
T,
SN, S, P) =
( { i, l, o, w }, { X, Y, S }, S, P)
Con las producciones:
P = { ( S ::= Xi ),
( Xi ::= wYo ),
( Y ::= iY ),
( Yo ::= l ),
( Y ::= l )}
Las derivaciones:
S --> Xi --> wYo --> wil
S --> Xi --> wYo --> wiYo --> wilo
Se genera el lenguaje de formato:
L = { wil, wilo, . . .}
Ejemplo 2:
La gramática
G = ( S T, SN, S, P)
= ( { a, c, i, o, r, p }, { X, Y, S }, S, P)
Con las producciones:
P = {( S ::= cX ),
( X ::= aX ),
( X ::= rY ),
( Y ::= pY ),
( Y ::= o ),
( pY ::= io )}
Las derivaciones:
S --> cX --> caX --> carY --> caro
S --> cX --> caX --> carY --> carpY --> carpio
Genera el lenguaje de formato:
L = { caro, carpio, . . .}
Ejemplo 3:
La gramática
G = ( S
T,
SN, S, P) = ( { 0, 1 }, { A, B, S }, S, P)
generará el lenguaje de formato:
L = { 11, 101 , 111, . . .},
si sus producciones son:
P = { ( S ::= A0 ), ( A ::= 1B1 ),
( 1 A ::= AB0 ),
( B ::= ℷ),
( B ::= 1 ), ( B ::= 0 )
Las derivaciones serán:
S --> AO --> 1B1 --> 1ℷ1 --> 11
S --> AO --> 1B1 --> 1B1 --> 101
S --> AO --> 1B1 --> 1B1 --> 111
Estas gramáticas irrestrictas, generan cualquier lenguaje formal irrestricto del tipo 0,
sobre un alfabeto S,
reconocidos por una Máquina de Turing,
que estructura frases sin restricciones
con el tipo de producciones: X=>Y,
donde:
- X:
Cadena no vacía de símbolos no terminales y/o terminales. - Y:
Cadena cualquiera de símbolos no terminales y/o terminales.
Para evitar la generación indiscriminada de palabras
insertando en cualquier tramo de una derivación una cadena Y,
en las producciones de estas gramáticas la parte:
- IZQUIERDA
no puede ser la palabra vacía l, así no habrán producciones de la forma l => Y. - DERECHA
puede ser la cadena vacía,
así habrán producciones de la forma Y =>,
así, si en el tramo de una derivación se produce
una secuencia que contenga la subcadena Y,
podrá eliminarse, reduciendo la longitud de la cadena durante una derivación.
Ejemplo 4:
Podrás verificar que la gramática
G = ( S
T,
SN, S, P) = ( { a }, { S,M,N,Q,R,T }, S, P)
Genera el lenguaje de formato:
L = { a2| Poencia + de 2},
si sus producciones son:
P = { ( S ::= MQaN ),
( Qa ::= MaQ ),
( QN ::= RN | T ),
( aR ::= Ra ),
( MR ::= MQ ),
( MT ::= ℷ)

EJEMPLOS LENGUAJE DEPENDIENTE DE CONTEXTO |
Ejemplo 1:
La gramática
G = ( S
T,
SN, S, P) = ( { i, l, o, w }, { X, Y, Z, S }, S, P)
Con las producciones:
P = { ( S ::= iXo ),
( iXo ::= iYl ),
( iYl ::= wiZl ),
( iYl ::= wil ),
( iZl ::= ilo)}
Las derivaciones serán:
S --> iXo --> iYl --> wil
S --> iXo --> iYl --> wiZl --> wilo
Se genera el lenguaje de formato:
L = { wil, wilo, . . .}
Ejemplo 2:
La gramática
G = ( S
T,
SN, S, P) = ( { a, c, i, o, r, p }, { X, Y, S }, S, P)
Con las producciones:
P = { ( S ::= cXo ),
( cXo ::= caXo ),
( aXo ::= arYo ),
( aXo ::= aro ),
( rYo ::= pYo),
( pYo ::= pio)}
Las derivaciones:
S --> cXo --> caXo --> caro
S --> cXo --> caXo --> carYo --> carpYo --> carpio
Genera el lenguaje de formato:
L = { caro, carpio, . . .}

EJEMPLOS LENGUAJE INDEPENDIENTE DE CONTEXTO |
Ejemplo 1:
La gramática
G = ( S
T,
SN, S, P) =
= ( { i, l, o, w }, { X, Y, S }, S, P)
Con las producciones:
P = {
( S ::= X ),
( X ::= wY ),
( Y ::= iY ),
( Y ::= lY ),
( Y ::= l ),
( Y ::= o )}
Las derivaciones serán:
S → X → wY → wiY → wil
S --> X --> wY --> wiY --> wilB --> wilo
Se genera el lenguaje de formato:
L = { wil, wilo, . . .}
Ejemplo 2:
La gramática
G =(ST,SN, S, P) = ( { a, c, i, o, r, p }, { X, Y, S }, S, P)
Con las producciones:
P = { ( S ::= cXo ), ( X ::= ar ),
( X ::= aYo ),( Y ::= pi )}
Las derivaciones serán:
S --> cXo --> caro
S --> cXo --> caYo --> carYo --> carpio
Se genera el lenguaje de formato:
L = { caro, carpio, . . .}
Ejemplo 3:
En la gramática
Para los parámetros:
- ST :
Símbolos terminales: { a, b } - SN :
Símbolos no terminales: { S, A } - S: Axioma
- P: Producciones
S --> aB|ba
A --> a | aS |bAA
B --> b | bS |aBB
Derivaciones:
Ejemplo:
S-->aB-->abS-->abba
Sea la GIC cuyas producciones son:
S --> AB;
A --> aA | a;
B --> bB | b
La gramática tendrá la forma
G = ( ST, SN, S, P )
cuyos elementos son:
ST :
Símbolos terminales: { a, b }
SN :
Símbolos no terminales: { S, A }
P: Producciones:
S --> A B
A --> a A | a
B --> b B | b
Sus derivaciones serán:
S ==> AB
AB==> AbB
AbB==> AbbB
AbbB==> Abbb
Abbb==> aAbbb
aAbbb==> aabbb
La cadena a a b b b
se derivará como:
S ==>AB==> AbB==> AbbB==> Abbb==> aAbbb==> aabbb
Lenguaje Independiente de contexto:
Aceptado por el Autómata de Pila, posee dos formatos equivalentes:
- Por vaciado de Pila:
El lenguaje aceptado es el conjunto de palabras que permite
transitar desde el estado inicial
hasta una descripción instantánea en la que tanto la entrada como la pila estén vacías.LV = { x | (q0, x, A0)|-*(q0, x, A0)
y ∈Q
y x∈S*}
Ejemplo
Un lenguaje aceptado por vaciado de pila sería:LV = {x(1+l)x-1|x=(0+1)+}
Intuitivamente, este autómata acepta ceros y unos en la entrada,
que va introduciendo en la pila por medio del
estado q0.En cualquier momento puede seguir leyendo la palabra x,
o empezar a leer la misma palabra de entrada,
pero al revés (su inversa)
y transitar al estado q1
que se encargará de comprobar que lee bien la inversa. - Por Estado Final:
El lenguaje aceptado por estado final es el equivalente al de los autómatas finitos,
todas las palabras que permiten transitar desde el estado inicial a uno final.Se aceptarán todas las palabras que
permitan pasar de la configuración inicial a una en la que se haya leído toda la palabra de entrada
y el autómata esté en uno de los estados finales,
independientemente del contenido de la pila.LEF =
{ x | (q0, x, A0)|-*(q0, ℷ, X)
y
p∈F , xÎS*y X∈ T*Los lenguajes de los autómatas
por vaciado de pila y
por estado final
son equivalentes,y siempre es posible obtener un AP
que reconozca por vaciado de pila
a partir de un AP que reconozca por estado final y viceversa.

EJEMPLOS LENGUAJE REGULAR |
La gramática G = ( S T, SN, S, P) = ( { i, l, o, w }, { X, Y, Z, S }, S, P)
Con las producciones:
- P = { ( S ::= X ), ( X ::= wX ), ( X ::= iY ),( Y ::= l ),( Y ::= lZ ),( Z ::= o )}
- Las derivaciones serán:
- S --> X --> wX --> wiY --> wil
- S --> X --> wY --> wiY --> wilZ --> wilo
Se genera el lenguaje de formato:
Ejemplo 2:
L = { wil, wilo, . . .}
La gramática G = ( S
T,
SN, S, P) = ( { a, c, i, o, r, p }, { X, Y, Z, S }, S, P)
Con las producciones:
- P = { ( S ::= X ), ( X ::= cX ), ( X ::= aY ),( Y ::= rY ),( Y ::= o ),( Y ::= pZ ),( Z ::= iZ ),( Z ::= o )}
- Las derivaciones serán:
- S --> X --> cX --> caY --> carY --> caro
- S --> X --> cX --> caY --> carY --> carpZ --> carpiZ --> carpio
Se genera el lenguaje de formato:
L = { caro, carpio, . . .}
Los LENGUAJES REGULARES
sobre un alfabeto S,
están formados por:
- El lenguaje vacío Ø,
- Los lenguajes unitarios, incluido { e }
- Los lenguajes obtenidos a partir de la concatenación A∩B,
- Los lenguajes obtenidos a partir de la unión AÈB
- Los lenguajes obtenidos a partir de la cerradura de estrella A* de lenguajes.
DEFINICION de
LENGUAJES REGULARES:
Son definidos recursivamente por las siguientes condiciones de recursividad:
- Ø Es un lenguaje regular
- {e}
Es un lenguaje regular - Para todo
a ∈S, {a}
es un lenguaje regular - Si A y B son lenguajes regulares,
entonces AÈB, A∩B y A*
son lenguajes regulares - Ningún otro lenguaje S es regular.
Luego, para el alfabeto
S = { a, b }
podemos afirmar que el lenguaje es regular:
- Ø y { e }
Porque cumple las condiciones 1 y 2 de la recursividad - {a} y {b}
Porque cumple la condición 3 de la recursividad - {a, b}
Porque cumple la condición 4, por existir unión de los lenguajes {a} y {b} - {a . b}
Porque cumple las dos razones anteriores - {a, ab, b}
Porque cumple las razones anteriores - { ai | i≥ 0 }
Porque cumple la Condición 4: ai es potencia iésima de {a} que es concatenación sucesiva - { ai bj | i ≥0, j≥0 }
Porque cumple las razones anteriores - { (ab)i | i≥ 0 }
Porque cumple las razones anteriores

LENGUAJE GENERADO por una GRAMATICA REGULAR |
Está formado por las cadenas generadas por las producciones de tal gramática;
o también podemos decir que L(G)
Está constituida por palabras obtenidas por aplicación de derivaciones
a partir del axioma de la gramática.
Este lenguaje, podemos representarlo en formato:
- L(G): FORMA SENTENCIAL:
- ST :
Símbolos terminales: { a, b } - SN :
Símbolos no terminales: { S, A } - S: Axioma: A
- P: Producciones
S --> b A
A --> a a A | b | ℷ - L(G): FORMA DE PARES:
- ST :
Símbolos terminales: { 0, 1 } - SN :
Símbolos no terminales: { A, B } - S: Axioma: A
- P: Producciones
{ ( A ::= 1B1 ), ( A ::= 0B0 ), ( B ::= A ), ( B ::= 1 ), ( B ::= 0 ), ( B ::= ℷ ) }
Representa a L(G)
bajo el formato S -->* x
donde x será la forma sentencial
si existe una derivación desde el axioma hasta esa palabra,
de esta manera al conjunto de todas las sentencias de la gramática L(G),
quedará representada como:
L(G) = { x | S -->*x, x ∈ST*}
En esta expresión diremos que
x es SENTENCIA
si es de forma sentencial
y todos sus símbolos pertenecen al alfabeto de símbolos terminales.
L(G): Ejemplo:
En la gramática
G = ( ST, NT, S, P )
Para los parámetros:
L(G)
contendrá todas las cadenas de forma:
b a2n b y b a2n
Lo cual significa que el lenguaje generado por la gramática será:
L(G) = b ( a2n ) * ( b È ℷ)
Deducimos de esta definición que
el lado derecho de una producción es una cadena que tiene la forma
ST *( SN ℷ ),
donde ℷ
puede ser el lado derecho de tal producción.
De manera que en el Ejemplo
S --> ℷ
indica que concluye la generación de la cadena,
y del mismo modo que la producción
A --> b
borrará el símbolo no terminal A.
En formato simplificado de pares de valores ( x, y ),
las producción se representan como
x --> y,
Los símbolos no terminales de SN
con las cadenas de
ST *( SN È ℷ),
Resultan los pares ordenados:
SN x ST *( SN È ℷ);
Así las producciones del Ejemplo
L(G) = b ( a2n ) * ( b È ℷ)
Representados como pares:
P = { ( S, b A ), ( A, a a A ), ( A, b ), ( A, ℷ) }
L(G): Ejemplo:
Dada la definición:
G = ( ST, SN, S, P )
Sea la gramática:
G1 = ( { 0, 1 }, { A, B }, A, P ),
para los pares de producciones
A ==> 1B1 1B1 ==> 1 ℷ 1 ==> 1 1 A ==> 1B1 1B1 ==> 101 A ==> 1B1 1B1 ==> 111
Genera el lenguaje de palabras palíndromos o simétricas.
L(G) = { 11, 101, 111, 00, 000, 010, 1001, 1111, 0000, 0110,…}
Producción que puede representarse como:
A ::= 1B1 | 0B0; B ::= A | 1 | 0 | ℷ
SENTENCIA:
Simbolizada como: S -->* x,
Para: x È ST*
Donde x es sentencia tiene forma sentencial y
todos sus símbolos pertenecen al alfabeto de símbolos terminales.
Así para la gramática anterior:
G 1 = ( { 0, 1 }, { A, B }, A, P)
Serán sentencias
0 1 0 y 1 0 0 1
pero no 1 A 1
Los lenguajes regulares son aceptados por las Máquinas de Estados Finitos,
las que se define como:
L(A)=(Q,S, q0,F, f)
Definido formalmente como:
L(G) = { w | S -->*w, w
ÎST* y f(q0, w) ∈ F)}
Dijo Dios al terminar de
crear al primer hombre
"Lo puedo hacer mejor"..
y creo a la mujer.!!
(Wilucha)


Gramáticas FORMALES
|
|||
|
Independiente del Contexto P = {( u::= v)| u = x Ay, u ∈ A+, v, x, y ∈ A*, A ∈ AN} |
Irrestricta P = {( u::= v)| u=x Ay, u ∈ A+, v, x, y ∈ A*, A ∈ AN } |
||
| Dependiente del Contexto P = {(S::=ℷ) o ( xAy::=xvy ) | x = y ∈ A*, A ÎSN, v ÎST+ } |
Regular:
Lineal por:
Izquierda: P={(S::=ℷ) o (A::=Ba) o (A::=a)| A, B ∈ SN, a ∈ ST+} Derecha: P={(S::=ℷ) o
|
||
- Parte del AXIOMA o símbolo inicial
- Detecta otros símbolos NO terminales, que son estados intermedios de generación.
- Luego, sobre los anteriores, efectua PRODUCCIONES que transforman sus símbolos no terminales.
- Concluye cuando la cadena queda constituida solo por símbolos terminales.

Las palabras sinceras no son elegantes
Las palabras elegantes, no son sinceras
Proverbio Chino

Formatos Gramaticales GRAMÁTICA IRRESTRICTA |
G = ( ST, SN, S, P)
Al generar una cadena, tiene un Símbolo Terminal a la izquierda, y a la derecha, un solo Terminal, que puede o no, estar seguido de un No terminal.
O sea que:
P = {( u::= v)|
u = x Ay, u Î A+, v, x, y Î
A*, A Î AN}
Ejemplo
La GI
G = (ST, SN, S, P)
= ( { i, l, o, w }, { X, Y, S }, S, P),
con las producciones:
P = {(S ::= Xi),(Xi::= wYo),
(Y::= iY),(Yo::= l),(Y::=l )}
Las derivaciones serán:
S --> Xi --> wYo --> wil
S --> Xi --> wYo --> wiYo --> wilo
Se genera el lenguaje:
L = { wil, wilo, . . .}
Ejemplo:
La GI
G = ( ST, SN, S, P)
= ( { a, c, i, o, r, p }, { X, Y, S }, S, P),
con las producciones:
P =
{(S ::= cX ),(X ::= aX),(X ::= rY),
(Y ::= pY ),( Y ::= o ),( pY ::= io )}
Las derivaciones serán:
S-->cX-->caX -->carY-->caro
S-->cX-->caX-->carY-->carpY-->carpio
Genera el lenguaje:
L = { caro, carpio, . . .}
Ejemplo:
La GI:
G = ( ST, SN, S, P)
= ( { 0, 1 }, { A, B, S }, S, P)
Genera el lenguaje:
L = { 11, 101 , 111, . . .},
Con producciones:
P = { ( S ::= A0 ), ( A ::= 1B1 ),
( 1 A ::= AB0 ),
( B ::= ℷ),
( B ::= 1 ), ( B ::= 0 )
Las derivaciones son:
S --> AO --> 1B1 --> 1ℷ1 --> 11
S --> AO --> 1B1 --> 1B1 --> 101
S --> AO --> 1B1 --> 1B1 --> 111
Ejemplo:
La GI
G3 = ( ST, SN, S, P )
= ( { 0, 1 }, { A, B, S }, S, P)
Genera el lenguaje de formato
L(G3) = { 11, 101 , 111},
Con producciones:
P = { ( S ::= A0 ), ( A 0 ::= 1B1 ),
( 1 A ::= AB0 ),(B ::= l ),
( B ::= 1 ), ( B ::= 0 ) }
Las derivaciones serán:
S=>AO=>1B1=>1l1=>11
S=>AO=>1B1=>101
S=>AO=>1B1=>111
Genera el lenguaje:
L(G3) = { 11, 101 , 111,...}
Una GI genera cualquier lenguaje formal irrestricto tipo 0, sobre un alfabeto S, reconocidos por una Máquina de Turing, que permiten estructurar frases sin restricciones con el tipo de producciones:
X =>Y , donde:
- X: Cadena no vacía de símbolos no terminales y/o terminales.
- Y: Cadena cualquiera de símbolos no terminales y/o terminales.
Para no generar un sin fin de cadenas insertando en cualquier tramo de una derivación una cadena Y,
en sus producciones la parte:
- Izquierda debe tener al menos un símbolo no terminal
- Derecha no requiere de ningún tipo de restricción.
P = { ( u::= v) |
u = x Ay, u Î A+, v, x, y Î
A*, A Î AN }
En la
- IZQUIERDA
no puede ser la palabra vacía l, así no habrán producciones de la forma l => Y.
- DERECHA
puede ser la cadena vacía, así habrán producciones de la forma Y =>,
así, si en el tramo de una derivación se produce una secuencia que contenga la subcadena Y,
podrá eliminarse, reduciendo la longitud de la cadena durante una derivación.
Ejemplo:
La gramática
G= ( S T
, SN, S, P )
= ( { a }, { S, M, N, Q, R, T }, S, P)
Genera el lenguaje:
G = ( ST,
SN, S, P)
Cuyas producciones: P al generar una cadena restringen a un solo Símbolo Terminal a la izquierda, y a derecha, un solo Terminal, que puede o no, estar seguido de un solo Símbolo No terminal.
Ejemplo: Con las producciones:
Genera el lenguaje:
Ejemplo: Con las producciones:
Las derivaciones serán:
S --> X --> cX --> caY --> carY --> Genera el lenguaje:
Ejemplo: Se la define como:
P: Producciones que para generar cada cadena,
tienen en cuenta lo que viene antes y después del símbolo que se sustituye.
P = { (S ::= ℷ) o ( xAy::=xvy ) |
Las derivaciones a partir de estas producciones, implican que las palabras generadas siempre tienen longitud mayor o igual que las anteriores en la derivación.
Ejemplo: Con las producciones:
Genera el lenguaje:
Ejemplo Con las producciones:
Las derivaciones:
Genera el lenguaje:
Ejemplo: Estas gramáticas son equivalentes pues generan el mismo lenguaje:
Gramáticas MENOS RESTRIGIDAS:
Las cadenas no vacías de terminales y no terminales, es la forma mas general,
de modo que las producciones podrían ser pares del producto
P = {( u::= v)|
Ejemplo
Las derivaciones serán:
Se genera el lenguaje:
Ejemplo:
P =
Las derivaciones serán:
Genera el lenguaje:
Ejemplo:
Genera el lenguaje:
Con producciones:
Las derivaciones son:
Ejemplo:
Con producciones:
Las derivaciones serán:
Genera el lenguaje:
Una GI genera cualquier lenguaje formal irrestricto tipo 0, sobre un alfabeto S, reconocidos por una Máquina de Turing, que permiten estructurar frases sin restricciones con el tipo de producciones:
X =>Y , donde:
Para no generar un sin fin de cadenas insertando en cualquier tramo de una derivación una cadena Y,
en sus producciones la parte:
P = { ( u::= v) |
En la
Ejemplo:
Genera el lenguaje:
G = ( ST,
SN, S, P)
Cuyas producciones: P al generar una cadena restringen a un solo Símbolo Terminal a la izquierda, y a derecha, un solo Terminal, que puede o no, estar seguido de un solo Símbolo No terminal.
Ejemplo: Con las producciones:
Genera el lenguaje:
Ejemplo: Con las producciones:
Las derivaciones serán:
S --> X --> cX --> caY --> carY --> Genera el lenguaje:
Ejemplo: Se la define como:
P: Producciones que para generar cada cadena,
tienen en cuenta lo que viene antes y después del símbolo que se sustituye.
P = { (S ::= ℷ) o ( xAy::=xvy ) |
Las derivaciones a partir de estas producciones, implican que las palabras generadas siempre tienen longitud mayor o igual que las anteriores en la derivación.
Ejemplo: Con las producciones:
Genera el lenguaje:
Ejemplo Con las producciones:
Las derivaciones:
Genera el lenguaje:
Ejemplo: Estas gramáticas son equivalentes pues generan el mismo lenguaje:
Gramáticas MENOS RESTRIGIDAS:
Las cadenas no vacías de terminales y no terminales, es la forma mas general,
de modo que las producciones podrían ser pares del producto
Se eliminan las restricciones para formar las producciones.
Donde:
P = { (S ::= ℷ) ó ( A ::= v ) |
Gramática de ESTRUCTURA de FRASES: GEF
Las producciones de la GEF, tienen el formato:
La GEF tiene en los lados izquierdos de P cualquier cadena no vacía sobre
NÈ å que contienen algún no terminal:
PÍ (NÈ å )*N(NÈ å )*
x (NÈ å )*
Se las conoce también como gramáticas no restringidas.
Las Gramáticas Dependientes de Contexto poseen GEF en las cuales las producciones se restringen a
a ->b tal que |a |>=|b |.
Su forma normal es
Lenguaje generado por una GIC
(PÍN x (å
ÈN)*)
Así para la
En síntesis toda gramática regular es una GIC
GIC: Ejemplo:
Sus elementos son:
Si consideramos la cadena aabbb sus derivaciones serán:
S=>AB
La cadena a a b b b se derivará como:
S=>AB=>AbB=>AbbB=>Abbb=>aAbbb=>aabbb
GIC: Ejemplo:
Con las producciones:
Se genera el lenguaje de formato:
GIC: Ejemplo:
Con las producciones:
Se genera el lenguaje de formato:
GIC: Ejemplo:
Para los parámetros:
Derivaciones:
GIC: Ejemplo:
S --> AB;
La gramática tendrá la forma
Sus derivaciones serán:
La cadena a a b b b se derivará como:
GIC: Ejemplo:
N={S}
Verifiquemos si la cadena aabb es generada o no por la GIC:
S=>aSb
Observemos que la cadena sí es generada por esta gramática,
GIC: Ejemplo:
Definimos las siguientes producciones
S-> xAy|ℷ
A-> xAy|ℷ
Definimos las producciones con el alfabeto ST = { x, y } para la condición m = 2n
S->x B y y | ℷ B-> x B y y | ℷ
La gramática buscada GIC = ( å, N, S, P ) donde å
= { x, y }, N = { S, A, B }, S el axioma y combina ambos conjuntos de producciones P:
S-> x A y | x B y y | ℷ
A-> x A y | ℷ
B-> x B y y | ℷ Limpiando estas producciones:
S-> x A y | x B y y | x y | x y y | ℷ A-> x A y | x y
ARBOLES de DERIVACION Para derivar una cadena a través de una GIC, el símbolo inicial se sustituye por alguna cadena.
El árbol tiene:
GIC: Ejemplo:
S->AC
Para la cadena aabbccc perteneciente a L(G),
S=>AC
S=>AC=>aAbC=>aabbC=>aabbcC=>aabbccC=>aabbccc Existen muchas derivaciones posibles para la cadena aabbccc,
S=>AC=>AcC=>AccC=>Accc=>aAbccc=>aabbccc
Estas derivaciones corresponden a la eleccion de distintos no terminales a expandir.
- En una derivacion por la izquierda
- En una derivacion por derecha
GIC: Ejemplo:
Ejemplo, dada la siguiente GIC G, donde:
La cadena "aabbb" perteneciente a L(G) puede formarse así:
S => AB => AbB => AbbB => Abbb => aAbbb => aabbb
Cuyo árbol de derivación asociado puedes apreciar al principio de este link.
AMBIGUEDAD:
P: S->aSa|aBa|b
Si analizamos las reglas de sustitución
En síntesis:
Y también:
Por consiguiente decimos que dicha gramática es Ambigua.
ANÁLISIS de AMBIGÜEDAD
Pero además,
Cuando en el árbol de derivación no se detectan estas falencias,
- Inexistencia de REGLAS NO GENERATIVAS,
- Ausencia de REGLAS DE REDENOMINACIÓN o PRODUCCIONES UNITARIAS,
Niveles de Ambigüedad
Ejemplo
La cadena 11 puede ser derivada como
Si todas las GIC para un lenguaje son ambigüas,
Ejemplo:
S=>SbS
=>SbScS
SbScS=>SbSca
Otras derivaciones posibles son:
S=>ScS=>
SbScS
SbScS=>abScS
S=>ScS=>SbScS=>abScS=>abacS=>abaca
Las cuales se corresponden con dos arboles distintos.
Consideremos la Gramática Independiente del Contexto
S->AB
La cadena: aabbb puede ser derivada mediante :
S=>AB=>AbB=>AbbB=>Abbb=>aAbbb=>aabbb El siguiente presenta el árbol de derivación:
Notar que los nodos hojas están etiquetados con símbolos terminales y leidas
de izquierda a derecha
Si la estructura de un lenguaje tiene más de una descomposición
Una gramática se dice que es ambigua
Ejemplo:
El árbol de derivación es:
S=>ScS=>SbScS=>abScS=>abacS=>abaca
Vemos que los dos árboles son distintos,
NORMALIZACION
L(G) = L(G').
Es decir, se obtendrá una nueva gramática,
El algoritmo que da solución a este planteo es:
Se pretende que todo símbolo terminal o no terminal de la nueva gramática (que será equivalente a la original),
Con esto se garantiza que todo terminal y no terminal es útil dentro de la gramática.
El algoritmo que da solución a este planteo es:
Si A -> w pertenece a P y además A pertenece a N':
Para ello, primero se identifica el conjunto Z de todos los no terminales anulables de una gramática
Identificados los no terminales anulables,
El primer paso para la aplicación de este algoritmo
Identificados los conjuntos unitarios de todos los no terminales de G = (N, E, S, P), se obtiene una gramática equivalente
- Inicializar P' = P.
TEORIA Tal cinta tiene una capacidad de almacenamiento ilimitada, porque no posee una celda primera ni ultima.
Para operar la cinta, tiene asociado un cabezal de lectura | escritura
Ejemplo:
Aplicando la definición:
Deducimos que sus parametros son:
Q : Conjunto Estados : { q 1, q 2, q 3, q 4 }
S : Alfabeto Entrada : { a }
T : Alfabeto Cinta : {a, ß }
s ' Q : Estado Inicial : q 1
ß ' T : Símbolo Blanco : ß
F Í Q : Datos de aceptación : { q4 }
d : Función Transición : d
Transforma (q,s) -> ( p, t, X )
q : Estado Actual
s : Símbolos de Cinta
p : Estado siguiente
t : Símbolo de la cinta
X : Movimiento del cabezal
Tabla de transiciones es:
d --- b
q1 -- q2aD q2bD
q2 -- q2aD q3bI
q3 -- q4aD q4bD
ALA, posee una arquitectura con una colección de celdas de extensión limitada.
Por ello necesitaremos otra máquina, como el autómata de pila,
TEOREMAS
El autómata de pila es la máquina que opera como una pila de datos y posee un mecanismo que le permite almacenamiento ilimitado, para contar o guardar los símbolos de las cadenas necesarias para efectuar comparaciones.
El AP opera en forma similar al AF, pues en todo momento se encuentra en un estado y el cambio de estado depende del estado actual y de una información adicional, que en el AF es el símbolo de entrada actual. El diagrama de transición para el lenguaje (a b )* es:
En el AP se incluye además del símbolo de entrada actual, el símbolo que está en ese momento en la cima de la pila. Por ello, cuando cambia de estado, el AP cambia también la cima de la pila.
A diferencia del "Autómata Finito. AF" que solo tiene capacidad para una "Memoria Finita", el AP puede reconocer cualquier LIC, para ello necesita guardar mucha información que usa para verificar, por Ejemplo cuantas aes preceden a las bes o contar la cantidad de aes para establecer las limitaciones, etc. Q: Estado S:Cinta T:Pila
q1
q2q3...qm
a1a2a3A0
A1A2A3
CONTROL: NO ACEPTA
Con color rojo marcamos el cabezal posicionado en ese elemento (símbolo de la cinta, estado actual o cima de la pila)
TRANSICIÓN:
Las transiciones que ejecutan los autómatas de pila siguen la siguiente secuencia:
DESCRIPCION INSTANTANEA:
Terna (q,x,z),
Movimiento: (q,ay,ZX) |-(p,y,xX) describe el paso de una descripción instantánea a otra.
Sucesión de Movimientos: (q,ay,ZX) |-*(p,y,xX) representa que desde la primera descripción instantánea se puede alcanzar la segunda.
METODOS DE ACEPTACIÓN:
TEOREMA:
El AP: autómatas de pila, que puede ser DETERMINISTA o NO DETERMINISTA,
Inicialmente la cinta tiene
Definición Formal:
Es una máquina que se define en términos de sus estados.
L = {an| n > 2 }
si sus producciones son
S=>MQaN
Qa=>MaQ
QN=>RN|T
aR=>Ra
MR=>MQ
aT=>Ta
MT=>l
Muchas palabras no indican
mucha sabiduría .!!
(Tales de Mileto)

GRAMATICAS REGULARES
N x S* ( N È e ).
Al lado izquierdo cada producción tiene un único símbolo no terminal,
y al derecho tiene cualquier cadena de terminales seguida por un no terminal.
El lenguaje
L(G) = { w | S -->*w, w ÎST*}
es Regular, si es generado por una Gramática Regular:
Estas producciones pueden ser:
P = { (S ::= ℷ) ó ( A ::= Ba ) ó ( A ::= a ) | A, B ÎSN, a ÎST+ }
P = { (S ::= ℷ) ó ( A ::= aB ) ó ( A ::= a ) | A, B ÎSN, a ÎST+ }
La gramática
G = ( S
T,
SN, S, P)
= ( { i, l, o, w }, { X, Y, Z, S }, S, P)
P = { ( S ::= X ), ( X ::= wX ),
( X ::= iY ),( Y ::= l ),
( Y ::= lZ ),( Z ::= o )}
Las derivaciones serán:
S --> X --> wX --> wiY --> wil
S --> X --> wY --> wiY --> wilZ --> wilo
L = { wil, wilo, . . .}
La gramática
G = ( S
T,
SN, S, P) =
( { a, c, i, o, r, p }, { X, Y, Z, S }, S, P)
P = { ( S ::= X ),
( X ::= cX ),
( X ::= aY ),
( Y ::= rY ),
( Y ::= o ),
( Y ::= pZ ),
( Z ::= iZ ),
( Z ::= o ) }
S --> X --> cX --> caY --> carY --> caro
carpZ --> carpiZ --> carpio
L = { caro, carpio, ..}
La gramática
G5 = ({0,1}, {A,B}, A, P)
No es del tipo 3, pues su parte derecha 2 de sus primeras reglas no cumplen con ninguna de las categorías de la gramática lineal;
en cambio
G6 =({ 0, 1},{A, B}, A, P)
Donde:
P ={(A::=1B), (B::=1), (B::=0C),(C::=1)}
Es equivalente a G5 por que genera el mismo lenguaje
L(G6) = L(G5) = { 11, 101 , 111}
Muchas palabras no indican
mucha sabiduría .!!
(Tales de Mileto)

GRAMATICA DEPENDIENTE del CONTEXTO
Solo admite como regla compresora
S ::= ℷ.
G = ( S
T,
SN, S, P)
x = y ∈ A*, A ÎSN, v ÎST+ }
La gramática
G = ( S
T,
SN, S, P)
= ( { i, l, o, w }, { X, Y, Z, S }, S, P),
P = { ( S ::= iXo ), ( iXo ::= iYl ),
( iYl ::= wiZl ),( iYl ::= wil ),
( iZl ::= ilo)}
Las derivaciones:
S --> iXo --> iYl --> wil
S --> iXo --> iYl --> wiZl --> wilo
L = { wil, wilo, . . .}
La gramática
G = ( S
T,
SN, S, P) =
( { a, c, i, o, r, p }, { X, Y, S }, S, P),
P = { ( S ::= cXo ), ( cXo ::= caXo ),
( aXo ::= arYo ),( aXo ::= aro ),
( rYo ::= pYo), ( pYo ::= pio)}
S --> cXo --> caXo --> caro
S --> cXo --> caXo --> carYo -->
carpYo --> carpio
L = { caro, carpio, . . .}
La gramática:
G3 = ( { 0, 1 }, { A, B, S }, S, P)
no es del tipo 1,
porque posee una regla compresora cuya parte izquierda no es el axioma
S ::= L;
En cambio:
G4 = ( { 0, 1 }, { A, B }, A, P )
es del tipo 1,
Donde:
P = { ( A ::= 1B1 ), ( A ::= 11 ), (1B1 ::= 101 ), ( 1B1 ::= 111 ) }
L(G4) = L(G3) = { 11, 101 , 111}
Aceptan en el lado izquierdo cadenas con no terminales, aún cadenas de no terminales y terminales.
( N È St>) o
(A::=aB) o (A::=a)|
A, B∈ SN, a ∈T+ }
La gramática, para operar las cadenas del lenguaje, efectua sobre su alfabeto el siguiente proceso:

Las palabras sinceras no son elegantes
Las palabras elegantes, no son sinceras
Proverbio Chino

Formatos Gramaticales
GRAMÁTICA IRRESTRICTA
G = ( ST, SN, S, P)
Al generar una cadena, tiene un Símbolo Terminal a la izquierda, y a la derecha, un solo Terminal, que puede o no, estar seguido de un No terminal.
O sea que:
u = x Ay, u Î A+, v, x, y Î
A*, A Î AN}
La GI
G = (ST, SN, S, P)
= ( { i, l, o, w }, { X, Y, S }, S, P),
con las producciones:
P = {(S ::= Xi),(Xi::= wYo),
(Y::= iY),(Yo::= l),(Y::=l )}
S --> Xi --> wYo --> wil
S --> Xi --> wYo --> wiYo --> wilo
L = { wil, wilo, . . .}
La GI
G = ( ST, SN, S, P)
= ( { a, c, i, o, r, p }, { X, Y, S }, S, P),
con las producciones:
{(S ::= cX ),(X ::= aX),(X ::= rY),
(Y ::= pY ),( Y ::= o ),( pY ::= io )}
S-->cX-->caX -->carY-->caro
S-->cX-->caX-->carY-->carpY-->carpio
L = { caro, carpio, . . .}
La GI:
G = ( ST, SN, S, P)
= ( { 0, 1 }, { A, B, S }, S, P)
L = { 11, 101 , 111, . . .},
P = { ( S ::= A0 ), ( A ::= 1B1 ),
( 1 A ::= AB0 ),
( B ::= ℷ),
( B ::= 1 ), ( B ::= 0 )
S --> AO --> 1B1 --> 1ℷ1 --> 11
S --> AO --> 1B1 --> 1B1 --> 101
S --> AO --> 1B1 --> 1B1 --> 111
La GI
G3 = ( ST, SN, S, P )
= ( { 0, 1 }, { A, B, S }, S, P)
Genera el lenguaje de formato
L(G3) = { 11, 101 , 111},
P = { ( S ::= A0 ), ( A 0 ::= 1B1 ),
( 1 A ::= AB0 ),(B ::= l ),
( B ::= 1 ), ( B ::= 0 ) }
S=>AO=>1B1=>1l1=>11
S=>AO=>1B1=>101
S=>AO=>1B1=>111
L(G3) = { 11, 101 , 111,...}
- X: Cadena no vacía de símbolos no terminales y/o terminales.
- Y: Cadena cualquiera de símbolos no terminales y/o terminales.
- Izquierda debe tener al menos un símbolo no terminal
- Derecha no requiere de ningún tipo de restricción.
u = x Ay, u Î A+, v, x, y Î
A*, A Î AN }
- IZQUIERDA
no puede ser la palabra vacía l, así no habrán producciones de la forma l => Y.
- DERECHA
puede ser la cadena vacía, así habrán producciones de la forma Y =>,
así, si en el tramo de una derivación se produce una secuencia que contenga la subcadena Y,
podrá eliminarse, reduciendo la longitud de la cadena durante una derivación.
La gramática
G= ( S T
, SN, S, P )
= ( { a }, { S, M, N, Q, R, T }, S, P)
L = {an| n > 2 }
si sus producciones son
S=>MQaN
Qa=>MaQ
QN=>RN|T
aR=>Ra
MR=>MQ
aT=>Ta
MT=>l
Muchas palabras no indican
mucha sabiduría .!!
(Tales de Mileto)

GRAMATICAS REGULARES
N x S* ( N È e ).
Al lado izquierdo cada producción tiene un único símbolo no terminal,
y al derecho tiene cualquier cadena de terminales seguida por un no terminal.
El lenguaje
L(G) = { w | S -->*w, w ÎST*}
es Regular, si es generado por una Gramática Regular:
Estas producciones pueden ser:
P = { (S ::= ℷ) ó ( A ::= Ba ) ó ( A ::= a ) | A, B ÎSN, a ÎST+ }
P = { (S ::= ℷ) ó ( A ::= aB ) ó ( A ::= a ) | A, B ÎSN, a ÎST+ }
La gramática
G = ( S
T,
SN, S, P)
= ( { i, l, o, w }, { X, Y, Z, S }, S, P)
P = { ( S ::= X ), ( X ::= wX ),
( X ::= iY ),( Y ::= l ),
( Y ::= lZ ),( Z ::= o )}
Las derivaciones serán:
S --> X --> wX --> wiY --> wil
S --> X --> wY --> wiY --> wilZ --> wilo
L = { wil, wilo, . . .}
La gramática
G = ( S
T,
SN, S, P) =
( { a, c, i, o, r, p }, { X, Y, Z, S }, S, P)
P = { ( S ::= X ),
( X ::= cX ),
( X ::= aY ),
( Y ::= rY ),
( Y ::= o ),
( Y ::= pZ ),
( Z ::= iZ ),
( Z ::= o ) }
S --> X --> cX --> caY --> carY --> caro
carpZ --> carpiZ --> carpio
L = { caro, carpio, ..}
La gramática
G5 = ({0,1}, {A,B}, A, P)
No es del tipo 3, pues su parte derecha 2 de sus primeras reglas no cumplen con ninguna de las categorías de la gramática lineal;
en cambio
G6 =({ 0, 1},{A, B}, A, P)
Donde:
P ={(A::=1B), (B::=1), (B::=0C),(C::=1)}
Es equivalente a G5 por que genera el mismo lenguaje
L(G6) = L(G5) = { 11, 101 , 111}
Muchas palabras no indican
mucha sabiduría .!!
(Tales de Mileto)

GRAMATICA DEPENDIENTE del CONTEXTO
Solo admite como regla compresora
S ::= ℷ.
G = ( S
T,
SN, S, P)
x = y ∈ A*, A ÎSN, v ÎST+ }
La gramática
G = ( S
T,
SN, S, P)
= ( { i, l, o, w }, { X, Y, Z, S }, S, P),
P = { ( S ::= iXo ), ( iXo ::= iYl ),
( iYl ::= wiZl ),( iYl ::= wil ),
( iZl ::= ilo)}
Las derivaciones:
S --> iXo --> iYl --> wil
S --> iXo --> iYl --> wiZl --> wilo
L = { wil, wilo, . . .}
La gramática
G = ( S
T,
SN, S, P) =
( { a, c, i, o, r, p }, { X, Y, S }, S, P),
P = { ( S ::= cXo ), ( cXo ::= caXo ),
( aXo ::= arYo ),( aXo ::= aro ),
( rYo ::= pYo), ( pYo ::= pio)}
S --> cXo --> caXo --> caro
S --> cXo --> caXo --> carYo -->
carpYo --> carpio
L = { caro, carpio, . . .}
La gramática:
G3 = ( { 0, 1 }, { A, B, S }, S, P)
no es del tipo 1,
porque posee una regla compresora cuya parte izquierda no es el axioma
S ::= L;
En cambio:
G4 = ( { 0, 1 }, { A, B }, A, P )
es del tipo 1,
Donde:
P = { ( A ::= 1B1 ), ( A ::= 11 ), (1B1 ::= 101 ), ( 1B1 ::= 111 ) }
L(G4) = L(G3) = { 11, 101 , 111}
Aceptan en el lado izquierdo cadenas con no terminales, aún cadenas de no terminales y terminales.
( N È S ) x S*
( N È e ).
Si se permitiera que en el lado izquierdo de una producción fuera la cadena vacía,
Se podría tener mas de un punto de partida para las derivaciones.
Por ello, no aceptaremos ℷ como lado izquierdo de una producción.
Muchas palabras no indican
mucha sabiduría .!!
(Tales de Mileto)

GRAMATICA INDEPENDIENTE del CONTEXTO
L(G) = { w | S -->*w, w ÎST*},
es un lenguaje independiente del contexto,
si es generado por una Gramática Independiente del Contexto
definida como:
G = ( ST,
SN, S, P)
P: Producciones que al generar una cadena a partir de otra, el símbolo terminal a transformar no depende de sus símbolos vecinos, tanto a la izquierda como a la derecha; por ello, al efectuar derivaciones para transformar un no terminal, no hace falta saber que hay alrededor de el.
A ÎSN, v ÎST+ }
La parte derecha son menos restrictiva, permiten pares del producto
N x S* ( N È e ).
Así, puede tener en la derecha, cualquier numero de símbolos no terminales,
y a la izquierda sigue restringido a un único no terminal.
Abarca:
- GIC: Gramática Independiente del Contexto
- GR: Gramática Regular
( N U S)* N ( N U S )* -> ( N U S )*.
Si a la gramática independiente de contexto se eliminan las restricciones del lado derecho de las producciones
se logra que la misma pueda estar formada por cualquier cadena sobre
NÈå.
a1Aa2->a1ba2
con b¹l ,
permite que el no terminal A sea reemplazado por b solo cuando
A aparezca en el contexto de a1 y a2.
Se simboliza L(G),
Es el lenguaje formado por todas las cadenas que se puedan derivar,
a partir del símbolo inicial, de las producciones de la
gramática independiente de contexto G
que tienen el siguiente formato:
GIC S-> aSb |ℷ
diremos que por inducción sobre n, se genera el
LIC = { an bn | n>=0 },
el cual no es un lenguaje regular,
por lo que podemos afirmar que
a pesar que el conjunto de lenguajes regulares
pertenecen al conjunto de LIC,
existen LIC que no son regulares.
y todo lenguaje regular es una LIC.
Sea la GIC cuyas producciones son:
S->AB; A->aA | a; B->bB | b
P: S->AB
A->aA|a
B->bB|b
AB=>AbB
AbB=>AbbB
AbbB=>Abbb
Abbb=>aAbbb
aAbbb=>aabbb
La gramática
G = ( S
T,
SN, S, P) = ( { i, l, o, w }, { X, Y, S }, S, P)
L = { wil, wilo, . . .}
La gramática
G = ( S
T,
SN, S, P) = ( { a, c, i, o, r, p }, { X, Y, S }, S, P)
L = { caro, carpio, . . .}
En la gramática:
G = ( ST, NT, S, P )
S --> aB|ba
A --> a | aS |bAA
S-->aB-->abS-->abba
Sea la GIC cuyas producciones son:
A --> aA | a
B --> bB | b
G = ( ST,
SN, S, P )
cuyos elementos son:
S --> A B
A --> a A | a
B --> b B | b
S ==>AB==> AbB==> AbbB==> Abbb==> aAbbb==> aabbb
Supongamos la gramática
G = ( N,å ,A ,P )
donde:
å ={a,b}
A=S (símbolo inicial)
P: S->aSb|ℷ( cadena vacia)
aSb=>aaSbb
aaSbb=> aabb
porque que al derivar desde el símbolo inicial S llegamos a una cadena de símbolos terminales.
Definir la GIC para el siguiente lenguaje
L={xn,ym | m,n>0 y m=n ó m=2n}
para el alfabeto
å={x,y}
para la condición: m = n
o ANALISIS:
Luego, los no terminales se van sustituyendo uno tras otro, por otras cadenas hasta que ya no quedan símbolos no terminales,
formándo finalmente una cadena con sólo símbolos terminales.
es decir, por un proceso equivalente,
se concluye que que hay más de un árbol de derivación posible
asociado a una misma cadena del lenguaje L(G);
que obligan a plantear el análisis correspondiente.
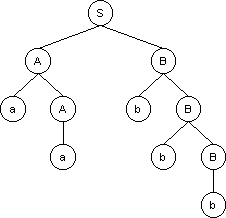
Contiene al símbolo inicial.
Contienen símbolos terminales y no terminales.
Son nodos que contienen símbolos no terminales.
Contienen símbolos terminales hojas.
Son las derivaciones se las representa por flechas.
Sea la gramática
G=(N,å, S,P) con N={S,A,C} ; å={a,b,c} ; S el símbolo inicial;
y cuyas producciones son:
A->aAb|ab
C->cC|c
Que genera el lenguaje
L(G)={ ai bic j | i>0 y j>=i}
tenemos la siguiente derivación:
AC=>aAbC
aAbC=>aabbC
aabbC=>aabbcC
aabbcC=>aabbccC
aabbccC=>aabbccc
su árbol de derivación seria:
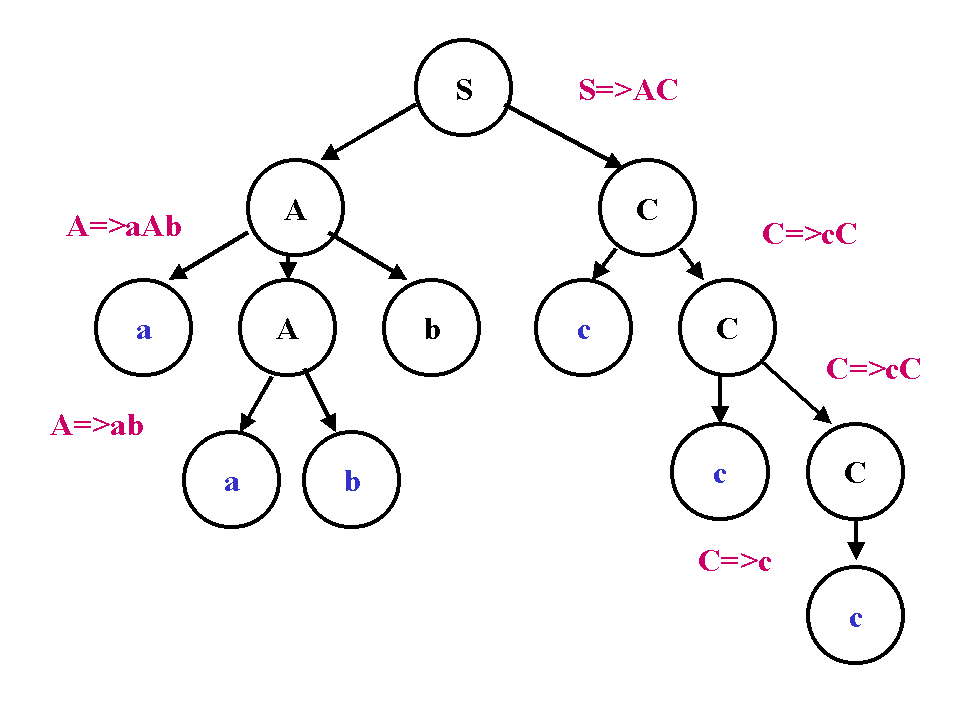
las cuales tienen el mismo arbol de derivacion anterior, por Ejemplo:
S=>AC=>AcC=>aAbcC=>aAbccC=>aAbccc=>aabbccc
El no terminal que se expande sera el que se encuentra mas proximo al extremo izquierdo.
El no terminal que se expande es el que se encuentra mas proximo al extremo derecho.

Cada cadena derivada mediante una GIC,
parte del símbolo inicial que da origen a las sucesivas derivaciones
quienes dan por resultado final tal cadena.
Para ello, uno y solo un no terminal es sustituido en cada producción,
por una cadena que puede formarse por terminales y/o no terminales.
Ejemplo:
La gramática definida por las producciones:
B -> b
para la cadena a a b a a
observaremos que puede ser generada por las siguientes derivaciones:
S=>aSa=>aaBaa=>aabaa

S=>aSa=>aaSaa=>aabaa
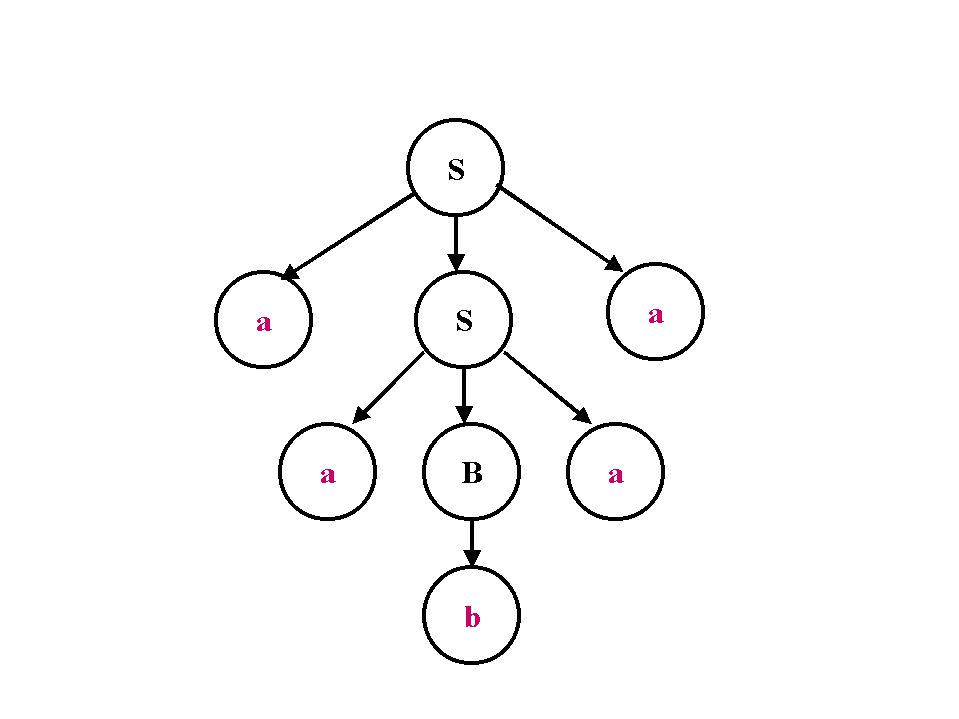
de una GIC:
Sus postulados son:
existe más de un árbol de derivación,
G se dice que es una GRAMÁTICA AMBIGUA.
existe solo un árbol de derivación,
se dice que G es una GRAMÁTICA NO AMBIGUA.
será un lenguaje ambiguo o un lenguaje no ambiguo
según el resultado del análisis de ambigüedad para G.
son ambiguas, se dice que el L
es un LENGUAJE INHERENTEMENTE AMBIGUO.
el árbol de derivación permite encontrar reglas de derivación
o símbolos no deseables en una GIC.
Tal es el caso de:
cuyas producciones no derivan en ninguna cadena de terminales
(NO terminales SIN DERIVACIÓN).
a los cuales nunca se puede llegar produciendo sobre S
(SÍMBOLOS INACCESIBLES).
se dice que la gramática es una GRAMÁTICA LIMPIA.
Sin embargo, para alcanzar la mejor de las condiciones (GRAMÁTICA BIEN FORMADA),
aun necesita verificar:
las cuales responden a la forma A -> ç, con ç palabra vacía y A distinto de S.
Cuando un no terminal que no es el símbolo inicial da lugar a una regla no generativa,
se conoce como NO TERMINAL ANULABLE.
las cuales se notan bajo la forma A -> B,
con A distinto de B y ambos pertenecientes a N.
Cuando existe mas de una derivación o árbol de derivación para una sentencia:
Sea la gramática
G6 = ( { 1 },{S, A }, S,{(S::=1A), (S::=11), (A::=1) } )
S=>1A=>11 ó S=>11
las cuales se representan por distintos arboles de derivación.
Cuando la gramática tiene en su estructura alguna sentencia ambigua.
Ejemplo:
La gramática anterior,
G6 = ( { 1 },{S, A }, S,{(S::=1A), (S::=11), (A::=1) } ),
debido a que existe una sentencia 11,
que al derivarse por medio de esta gramática, es ambigua.
Se presenta cuando un lenguaje es generado por una gramática ambigua.
Ejemplo:
Como la gramática es ambigua,
G6 = ( { 1 },{S, A }, S,{(S::=1A), (S::=11), (A::=1) } )
es ambigua,
el lenguaje L(G6)={11} es ambiguo.
se dice que el lenguaje es un lenguaje independiente del contexto (LIC) inherentemente ambigüo.
Para la GIC:
S->S b S | S c S | a
y la cadena abaca,
podemos graficar dos árboles distintos pero producen la misma cadena.
Unas derivaciones posibles son:
SbSca=>Sbaca
Sbaca=>abaca
S=>SbS=>SbScS=>SbSca=>Sbaca=>abaca
abScS=>abacS
abacS=>abaca
G = ( N, å, S,P)
con N = { S, A, C } ;
å = {a, b, c} ; S el símbolo inicial;
y cuyas producciones son:
A->aAb|ab
B->bB|b
Comenzamos en la raíz S
y generamos los hijos A y B.
A y B son raíz del subárbol correspondiente a la parte de la cadena final que ellos generan.
se obtiene la cadena aabbb.
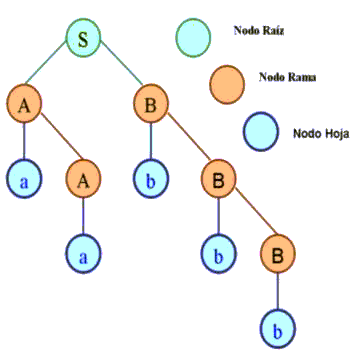
y si la construcción final determina su significado,
entonces el significado es ambiguo.
si hay dos o más árboloes de derivación distintos para la misma cadena.
Supongamos la gramática:
P: S->SbS|ScS|a
Podemos derivar la cadena abaca
de dos formas distintas:
S=>SbS=>SbScS=>SbSca=>Sbaca=>abaca
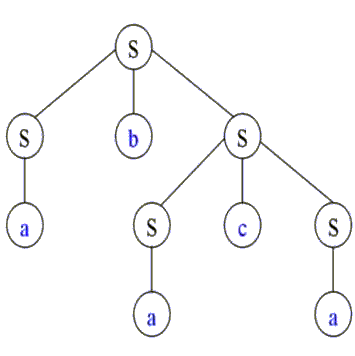
El árbol de derivación es:
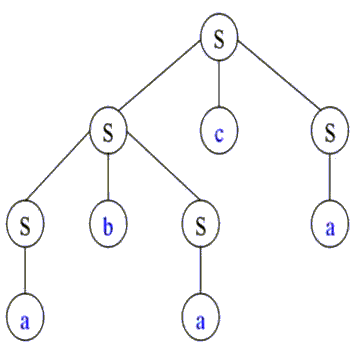
aunque las cadenas producidas son las mismas.
Por tal razón diremos que la gramática es ambigüa.
La GIC proporciona escaso control sobre las producciones permitidas y ello,
da lugar a la presencia de símbolos y producciones no deseables,
que permiten la existencia de árboles de derivación demasiado profundos,
demasiado anchos e incompletos.
A fin de evitar tales inconvenientes,
convendría establecer restricciones que no limiten la capacidad generativa de la GIC,
para generar su forma normales o su modelo formal estándar,
del cual resulten gramáticas bien formadas que limiten los árboles innecesariamente complejos o inútilmente sencillos.
Para lograr tal forma normal,
debemos aplicar las siguientes técnicas específicas de los algoritmos de limpieza Gramátical.
NO terminales SIN DERIVACIÓN
Sea
G = ( N, S , S, P ) una GIC.
Será transformada en G' = ( N', S , S, P' )
de modo tal que:
Para todo A perteneciente a N', A =>* w, w perteneciente a S * .
la cual será equivalente a la original,
pero que la perfeccionará en el sentido de que en la nueva gramática,
todos los no terminales,
acabarán por derivar (=>*) en cadenas formadas solo por símbolos terminales
(es decir, completarán su proceso de derivación).
Con esto se soluciona el "problema del árbol incompleto".
para los cuales
A -> w es una producción de G con w ∈ S *.
para las cuales
A ∈ a N' y w ∈ S *.
- Añadir a N' todos los no terminales A
para los cuales A -> w sea una producción de P
tal que w ∈ ( N' U S )*.
- Añadir esa producción A -> w a P'.

NO terminales y terminales INACCESIBLES
Sea
G = (N, E, S, P) una GIC.
Será transformada en
G' = (N', E', S, P') de modo tal que:
- L(G) = L(G').
- Para todo X perteneciente al conjunto (N' u E'),
S =>+ wXw',
para las subcadenas w y w' de la forma (N' u E')*.
pueda ser alcanzado a partir de sucesivas derivaciones (=>+)
que se apliquen sobre S.
- Inicializar N' = {S} y P' = E' = {} (conjuntos vacíos).
- Repetir hasta que no se puedan añadir nuevas producciones:
- Agregar A -> w en P'.
- Para todo terminal x de w, introducirlo en E'.
- Para todo no terminal X de w, introducirlo en N'.
DE NO terminales ANULABLES
Un no terminal que verifica
A =>* ç se dice "anulable".
El único caso en que estos terminales son deseables es cuando ç pertenece a L(G);
sin embargo, la única producción necesaria y deseable para que esto ocurra es
la producción S -> ç.
Entonces, todas las demás producciones de este tipo deben eliminarse de la gramática.
mediante el siguiente algoritmo:
- Inicializar Z con todos los no terminales A para los cuales existe la producción de la forma A -> ç.
- Repetir hasta que no puedan añadirse más no terminales a Z:
Si B -> w tal que w pertence a (N u E)*
y todos los símbolos de w están en Z, agregar B en Z.
para todas las producciones
B -> X1X2...Xn
pertenecientes a P,
se agrega en P' todas las combinaciones posibles
de B -> Y1Y2...Yn tal que:
- Con Xi no anulable, solo se considere Yi = Xi.
- Con Xi anulable,
se consideren las posibilidades Yi = Xi
y además
Yi = ç.
Es decir, un anulable en P da lugar a dos producciones en P'.
- Yi no es ç para todo i
(si así lo fuera, se estaría introduciendo una producción ç).
PRODUCCIONES UNITARIAS
El último algoritmo de limpieza,
simplifica derivaciones de la forma
A1 => A2 => ... => An
generando la producción A -> An.
Es decir, evita que el árbol de derivación sea innecesariamente delgado y profundo.
es la definición del CONJUNTO UNITARIO de cada no terminal A,
definido este como el conjunto de símbolos no terminales B
tal que según P, exista la producción
A =>* B
utilizando solo producciones unitarias.
Por definición, el primer elemento del conjunto Unitario(A) es el elemento {A}.
G' = (N, E, S, P')
de modo que P' no contiene producciones unitarias:
- Para cada A perteneciente a N para el cual Unitario(A) sea distinto de {A}
- Para cada B ( Unitario(A)
- Para cada producción no unitaria B -> w de P, agregarla en P' bajo la forma A -> w.
- Eliminar todas las producciones unitarias en P'.

La inteligencia artificial
jamas superará a la
estupidez humana
Wilucha


de los
A U T O M A T A S
El autómata es un mecanismo analítico que actua como una máquina automática, programada para procesar las cadenas de un lenguaje
Es una especie de algoritmo operativo que emula un elemento motriz para funcionar como auditor gramátical.
de Turing
Definiciòn
MT = ( Q, S, T, s, ß, F, d )
Lineal Acotado
Definiciòn
ALA = ( Q, S, T, <, >, s, ß, F, d )
de Pila
Definición:
AP = ( S, T, Q, Ao, qo, F, d )
Puede ser:
- Determinista
- No Determinista
Finito
A = ( Q, S, d, q0, <, >, F )
SECUENCIAL
- Máquinas: Mealy y Moore
FINITO
- Determinista y No Determinista
AUTOMATA: Probabilístico, de Células, de McCulloch-Pitts.
MÁQUINA de TURING
Autómata LINEAL ACOTADO
Autómata DE PILA
Determinista
No Determinista
Autómata FINITO
Determinista
No Determinista
de McCulloch-Pitts.
Aprender es como remar
contra la corriente
Si no se avanza,
se retrocede...!
Proverbio chino

AUTÓMATAS
MAQUINA de TURING MT
Cuenta con una cinta infinita en ambas direcciones. Sobre ella, posee una colección de celdas contiguas capaces de
almacenar un símbolo cada una.
Los contenidos de las celdas pueden accederse en cualquier orden.
- Que puede moverse sobre la cinta y
- En cada movimiento lee o escribe un símbolo.
Arquitectura MT
Definiciòn:
MT = ( Q, S, T, s, ß, F, d )
Cinta S:
| a1| a2 | a3 |...| an |...
/\
<- / d \ -> Cabezal
| q1 |
| q2 |
| q3 |
.
.
| qm |
Estados: Q
Q : Conjunto Estados : { q1, q2, q3, . . . }
S : Alfabeto Entrada : { a1, a2, a3, a4, . . . }
T : Alfabeto Cinta :
s ∈ Q : Estado Inicial :
ß ∈ T : Símbolo Blanco :
F Í Q : Datos de aceptación :
d : Función Transición :
Que transforma (q,s) -> ( p, t, X )
q : Estado Actual
s : Símbolos de Cinta
p : Estado siguiente
t : Símbolo de la cinta
X : Movimiento del cabezal
Sea la máquina MT1 definida como:
MT1 =
( { q 1,q 2, q 3, q 4 },
{ a }, { a, ß }, q 1, ß,
{ q 4}, d )
M =
( Q, S, T, s, ß, F, d )
Antes de nuestra venida
nada le faltaba al mundo;
Despues de nuestra marcha,
nada le faltará..!!
Proverbio Persa

AUTÓMATAS
AUTOMATA LINEALMENTE ACOTADO
Consiste en un conjunto finito de estados, un alfabeto finito de la cinta que incluye
los símbolos marcadores < y >, que delimitan la cinta ,un estado inicial y
un conjunto de instrucciones similares a la máquina de Turing.
El alfabeto de entrada estará escrito entre los marceadores < y >
El ALA no contiene instrucciones para moverse después de ellos, ni borrarlos,
ni reemplazarlos.
El funcionamiento del ALA requiere que se encuentre en un estado y el cambio de estado depende del:
a) Estado actual en el que se encuentra y
b) Símbolo leído de la cinta de entrada
La cinta estará asociada con un cabezal de lectura /escritura que no podrá moverse mas allá de los marcadores.
- Es de longitud limitada, por eso se definen dos marcadores de la cinta que delimitaran el principio y el fin.
- Contiene los caracteres de entrada a1 Î å
Es de lectura y escritura, que:
- No puede desplazarse mas a la izquierda del símbolo que delimita la izquierda,
- Ni mas a la derecha del símbolo que delimita la derecha.
Cada movimiento es registrado por un estado.
Administra los movimientos del autómata, que depende del
- Estado actual en el que se encuentra y del
- Símbolo de la cinta.
Arquitectura ALA
Definiciòn
ALA = ( Q, S, T, <, >, s, ß, F, d )
Cinta S:
| < | a1| a2 | a3 |...| an |...| > |
/\
<- / d \ -> Cabezal
| q1 |
| q2 |
| q3 |
.
.
| qm |
Estados: Q
Q : Conjunto Estados : { q1, q2, q3,...}
S : Alfabeto Entrada: { a1, a2, a3, a4,...}
T : Alfabeto Cinta: {<, a1, a2, a3, a4,... >}
s ∈ Q: Estado Inicial :
ß ∈ T: Símbolo Blanco :
F Í Q: Datos de aceptación :
d: Función Transición :
Que transforma (q,s) -> ( p, t, X )
q : Estado Actual
s : Símbolos de Cinta
p : Estado siguiente
t : Símbolo de la cinta
X : Movimiento del cabezal
Antes de nuestra venida
nada le faltaba al mundo;
Despues de nuestra marcha,
nada le faltará..!!
Proverbio Persa

AUTÓMATAS
AUTOMATA DE PILA
organizada como una colección de celdas contiguas capaces de almacenar cada una, un único símbolo,
al que puede accederse solamente en un solo sentido,
mediante una cabeza de solo lectura,
que puede moverse sobre la cinta y por cada movimiento lee un solo símbolo.
Arquitectura AP
Definición:
AP = ( S, T, Q, Ao, qo, F, d )
Cinta:
S:
| a1 | a2| a3|...| an |...
/\Cabezal
/ d \ ->
| q1 |
| t0 |
| q2 |
| t1 |
| q3 |
| t2 |
.
.
| qm |
| ti |
Estados: Q Pila: T
Q : Conjunto Estados :
{ q1, q2, q3, . . . }
S :Alfabeto Entrada:
{ a1, a2, a3, a4, . . . }
T : Alfabeto de símbolos de pila
qo : Estado Inicial
F : Conjunto de estados finales
d : Función Transición :
( qi, ai , ti ) -> ( qi+1, ti+1 )
qi : Estado Actual
ai : Símbolos Actual leido en Cinta
ti : Símbolo leido en la cima de pila
Para procesar una LIC de la forma
{ an bn |n > 0 }
precisaríamos memoria para un contador de
aes, luego memoria para verificar que todas las
a
es precedan a las bes,
por lo tanto, la única memoria del autómata finito, nos resultaría insuficiente.
con memoria para registrar tanto la cantidad de símbolos y otra para guardar tales símbolos.
El funcionamiento requiere que el AP esté se encuentre siempre en un estado.
El cambio de dicho estado depende del:
Estado actual.
Símbolo leído en la entrada.
Símbolo que en ese momento está localizado en la cima de la pila
Cuando cambia de estado también cambia tal símbolo de la cima.
Para operar esta estructura gráfica de modo más simple, consideraremos la siguiente representación literal:
f(q,a,Z)={(q1,z1), (q2,z2),...,(qn,zn)}
(q,a,Z; qn,yn)
Permite describir sencillamente la configuración del AP en cada momento.
q∈Q, xÎS*, z∈T*
contiene el estado actual,
la palabra que queda por leer y el símbolo en la cima de la pila.
Cada transición reclama un símbolo en la pila, por tanto si esta queda vacía el autómata se detiene y esta expresión indica que puede ocurrir que:
- El AP puede terminar o no con la pila vacía , en el caso de que vacíe su pila a cadena es Aceptado por Vaciado de Pila.
- La aceptación requiere que el AP se mueva a un estado final cuando la cadena de la cinta se agote.
Para cada autómata de pila que acepte cadenas sin vaciar su pila,
existe un autómata equivalente pero que vacía su pila antes de llegar a un estado de aceptación
en función de la estructura de sus transiciones de un estado a otro.
Antes de nuestra venida
nada le faltaba al mundo;
Despues de nuestra marcha,
nada le faltará..!!
Proverbio Persa

AUTÓMATAS
AUTÓMATA FINITO
El AUTÓMATA FINITO:
- Tiene una cinta de infinita hacia la derecha
- Con un cabezal capaz de realizar solamente la operación de lectura,
- Lee un símbolo de la cinta de entrada
- y se desplaza un lugar hacia la derecha.
- una secuencia cualquiera de símbolos de entrada seguida de espacios en blanco,
- el cabezal de esta cinta se encuentra sobre el primer símbolo de la secuencia de entrada.
Un autómata finito es una quíntupla,
- es un mecanismo automático para verificar si una cadena pertenece o no a un determinado lenguaje,
- es decir una estructura algebraica
- A =
- que determina el único estado siguiente para el par (qi , s) correspondiente al estado actual y a la entrada.
Los Autómatas Finitos son una subclase de lasMáquinas Secuenciales, pues, la principal diferencia está en que la salida, está limitada a dos valores: aceptada la palabra o no aceptada.
Los Autómatas Finitos transitan entre estados de un conjunto de estados según reciben los símbolos que forman la palabra de entrada.
Hay tres tipos de estados:
que permite empezar la ejecución del Autómata
que permiten realizar la salida de aceptación de la palabra de entrada en él caso de que no haya mas símbolos en la entrada.
El cambio de estado depende de la entrada y del estado en que se encuentre.
El Autómata Finito, es una computadora ideal.
Pueden usarse para diseñar analizadores léxicos de los compiladores, circuitos electrónicos, editores de texto, etc.
Segun cómo se defina su capacidad para cambiar de estado se clasifican en dos tipos:
- Deterministas
- No deterministas
Los humanos tienen que respirar ...
y las empresas tienen que generar dinero.!!
(Wilucha)

COMPILADORES
Abarca:
son:
Código
Léxico
Sintáctico

C O M P I L A D O R E S VOCABULARIO BÁSICO |
- TRADUCTOR:
Programa computacional que toma como entrada un texto escrito en un lenguaje llamado "Lenguaje Fuente" y produce como salida otro texto en un lenguaje, denominado "Lenguaje Objeto".Texto Lenguaje Fuente -> TRADUCTOR -> Texto Lenguaje Objeto
- COMPILADOR:
Traductor cuyo lenguaje fuente es un lenguaje de programación de alto nivel y la salida es un lenguaje de bajo nivel o ensamblador o código de máquina; así, genera un programa ejecutable a partir de un programa fuente en el lenguaje de alto nivel - LINKER:
Construye un fichero ejecutable añadiendo al fichero objeto generado por el compilador las cabeceras necesarias y las funciones de librería utilizadas por el programa fuente. - DEPURADOR:
Permite seguir paso a paso la ejecución de un programa, siempre que el compilador haya generado adecuadamente el programa objeto. - ENSAMBLADOR:
Compilador cuyo lenguaje fuente es el lenguaje ensamblador. Algunos compiladores, en vez de generar código objeto, generan un programa en lenguaje ensamblador que debe después convertirse en un ejecutable mediante un programa ensamblador. - INTERPRETE:
A diferencia del compilador que genera un programa equivalente, este toma una sentencia del programa fuente en lenguaje de alto nivel y luego la traduce al código equivalente y al mismo tiempo lo ejecuta.
COMPILAR O INTERPRETAR?
Ventajas de compilar frente a interpretar:
- Se compila una vez, se ejecuta varias veces.
- La compilación de bucles genera código equivalente al bucle, pero interpretándolo se traduce tantas veces una línea como veces se repite el bucle.
- La información de mensajes de error es más detallada, por que el compilador tiene vista global del programa.
Ventajas del intérprete frente al compilador:
- El intérprete requiere menos memoria que un compilador.
- En tiempo de desarrollo, permite más interactividad con el código.
Quien no calla el hecho,
tampoco callará su autor..!!
Séneca

C O M P I L A D O R E S T I P O S |
- ENSAMBLADOR:
- COMPILADOR CRUZADO:
- COMPILADOR CON MONTADOR:
- AUTOCOMPILADOR:
- METACOMPILADOR:
- DESCOMPILADOR:
El lenguaje fuente es lenguaje ensamblador y posee una estructura sencilla.
Genera código en lenguaje objeto para una máquina diferente de la que se está utilizando para compilar. Es perfectamente normal construir un compilador de Pascal que genere código MS- DOS y que el compilador funcione en Linux y se haya escrito en C++.
Compila distintos módulos de forma independiente y después es capaz de enlazarlos.
Compilador escrito en el mismo lenguaje que se va a compilar, por tanto no puede ejecutarse la primera vez. Sirve para ampliar lenguajes, mejorar el código generado, etc.
Compilador de compiladores, es un programa que recibe como entrada las especificaciones del lenguaje para el que se desea obtener un compilador y genera como salida el compilador para ese lenguaje.
Programa que acepta como entrada código máquina y lo traduce a un lenguaje de alto nivel, realizando el proceso inverso a la compilación.
Lenguaje Fuente ? COMPILADOR ? Lenguaje Objeto
La descompilación es factible si el programa objeto se guarda la tabla de símbolos y si no se hizo optimización de código.
Por ello existen más que buenos descompiladotes, buenos desensambladotes.

C O M P I L A D O R E S E T A P A S |
PROGRAMA FUENTE
|
| Análisis Léxico |
| Análisis Sintáctico |
Tabla de > | Análisis Semántico | > Manejo de
Símbolos | Generar código Intermedio | errores
| Optimización de Código |
| Generación de Código |
|
PROGRAMA OBJETO
Gracias a los sistemas de memoria virtual, el fichero ejecutable del compilador es relativamente pequeño comparado con el de otros programas del sistema,
por tanto para compilar un programa medio ya no existen los viejos problemas de escasez de memoria.
Se tiende a reducir el número de ficheros leídos o escritos para reducir el numero de pasadas, incluso en las realizadas en memoria, sin escribir ni leer nada del disco, así se disminuye el tiempo destinado a escribir y leer un fichero de tamaño similar o mayor que el de programa fuente en cada fase.
Las fases se agrupan en dos partes o etapas:
- FRONT END:
- BACK END:
Fase de análisis, que depende del lenguaje fuente y es independiente de la máquina objeto para que la que se va a generar el código.
Fase de generación y optimización de código que depende del lenguaje objeto y debe ser independiente del lenguaje fuente.
Ambas etapas se comunican mediante una representación intermedia generada por el frond end, que puede ser una representación de la sintaxis del programa o bien puede ser un programa en un lenguaje intermedio.

C O M P I L A D O R E S ANALISIS LEXICO o SCANNER |
En esta fase se manejan los siguientes conceptos:
- TOKENS:
- TIRAS ESPECÍFICAS:
- TIRAS NO ESPECÍFICAS:
- PATRÓN:
- LEXEMA:
- ATRIBUTOS:
Símbolos terminales de cada gramática como palabras reservadas, identificadores, signos de puntuación, constantes numéricas, operadores, cadenas, etc. Existen tokens con varios signos, como “: =”, “= =”, “+ =”, “???”, etc. Los tokens que tiene dos componentes: Tipo y Valor, pueden estar constituidas por:
Son las palabras reservadas, if then else, function, while, etc, el punto y coma, la asignación, los operadores aritméticos o lógicos, etc. Estas tiras sólo tienen tipo.
Constituidas por los identificadores, constantes o etiquetas. Estas tiras tienen tipo y valor. Por Ejemplo, si “contador” es un identificador, el tipo de token será identificador y su valor será la cadena “contador”.
Expresión regular que define el conjunto de cadenas que puede representar a cada uno de los tokens.
Cadena que se produce al analizar el texto fuente y encontrar una cadena de caracteres que representan un token determinado. Así, el lexema es una secuencia de caracteres del código fuente que concuerda con el patrón de un token.
Información adicional sobre los tokens en forma de atributos asociados, cuyo número de depende de cada token; aunque en la práctica el único atributo es el registro que contiene la información propia como, lexema, tipo de token y línea y columna en la que fue encontrado.
En la misma pasada el AL puede funcionar como subrutina del analizador sintáctico, es la etapa del compilador que identifica el formato del lenguaje, leyendo para ello, los caracteres del programa e ignorando sus elementos innecesarios para la siguiente fase, como tabuladores, comentarios, espacios en blanco, etc.
El AL agrupa por categorías léxicas los caracteres de entrada, estableciendo el alfabeto con el que se escriben los programas válidos en el lenguaje fuente y rechaza cadenas con símbolos ilegales del alfabeto, desarrollando para ello las siguientes operaciones:
- PROCESO LÉXICO DEL PROGRAMA FUENTE: Identificador de tokens y de sus lexemas que deberán entregar al analizador sintáctico e interaccionar con la tabla de símbolos.
- MANEJA EL FICHERO DEL PROGRAMA FUENTE; Abre, lee sus caracteres y cierra.
- IGNORA COMENTARIOS: Como separadores, espacios blancos, tabuladores, retornos de carro, etc.
- LOCALIZA ERRORES: Cuando se produce un error sitúa la línea y la posición en el programa fuente y registra las líneas procesadas.
- PROCESO DE MACROS, definiciones, constantes y órdenes de inclusión de otros ficheros.
Para reconocer un tokens el AL lee los caracteres hasta llegar a uno que no pertenece a la categoría del token leído, el último carácter es devuelto al buffer de entrada para ser leído en primer lugar en la próxima llamada al analizador léxico. Cuando el AS vuelve a llamar al AL, éste lee los caracteres desde donde quedó en la llamada anterior, hasta completar un nuevo token y devolver el par Token - Lexema.
El funcionamiento de una analizador léxico puede representarse mediante la máquina de estados, llamada diagrama de transición (DT), muy parecida a un autómata finito determinista.
CREACION DE
ANALIZADORES LEXICOS:
Las alternativas son:
- USAR UN GENERADOR AUTOMÁTICO
de analizadores léxicos, como el LEX: su entrada es un código fuente con la especificación de las expresiones regulares de los patrones que representan a los token del lenguaje, y las acciones a tomar cuando los detecte. - ESCRIBIR el AL en LENGUAJE DE ALTO NIVEL
de uso general utilizando sus funciones de E/S. - HACERLO EN LENGUAJE ENSAMBLADOR.
ERRORES LEXICOS
Los errores característicos detectados por el analizador léxico son:
- Uso de caracteres que no pertenecen al alfabeto del lenguaje (“ñ” o”?”).
- Palabras que no coinciden con ninguno de los patrones de los tokens posibles
La detección de un error puede implicar:
- Ignorar los caracteres no válidos hasta formar un token según los patrones dados;
- Borrar los caracteres extraños;
- Insertar un carácter que pudiera faltar;
- Reemplazar un carácter presuntamente incorrecto por uno correcto;
- Conmutar las posiciones de dos caracteres adyacentes.

C O M P I L A D O R E S ANALISIS SINTACTICO AS o PARSER |
construye una representación interna del programa o caso contrario enviar un mensaje de error.
Comprueba si los token van llegando en el orden definido,
para luego generar la salida con formato de árbol sintáctico.
Me modo que sus funciones serán:
- Aceptar solo lo que es válido sintácticamente.
- Explicitar el orden jerárquico que tienen los operadores en el lenguaje de que se trate.
- Guiar el proceso de traducción dirigida por la sintaxis.
A partir del árbol sintáctico que representa la sintaxis de un programa, el AS construye una derivación con recorridos por la izquierda o por la derecha del programa fuente, y partir de ellos construye una representación intermedia de ese programa fuente, que puede ser un árbol sintáctico abstracto o bien un programa en un lenguaje intermedio.
hay dos estrategias para construir el árbol sintáctico:
- ANÁLISIS DESCENDENTE:
Opera desde la raíz de árbol y va aplicando reglas por la izquierda, de forma de obtener una derivación por izquierda de la cadena de entrada.
Recorriendo el árbol en profundidad de izquierda a derecha, encontraremos en las hojas los tokens, que nos devuelve el A.L. en ese mismo orden. - ANÁLISIS ASCENDENTE:
Desde la cadena de entrada se construye el árbol empezando por las hojas, luego se crean nodos intermedios hasta llegar a la raíz; construyendo así al árbol de abajo hacia arriba.
El recorrido se hará desde las hojas a la raíz.
El orden en el que se van encontrando las producciones corresponde a la inversa de una derivación por la derecha.
La pluma puede llegar a ser
más cruel que la espada..!!
(Robert Burton)

C O M P I L A D O R E S ANALISIS SEMÁNTICO |
En caso del símbolo único con varios significados u operador polimórfico, el análisis semántico determina cuál es aplicable; así, para el signo “+”, que permite sumar números, concatenar cadenas de caracteres y unir conjuntos,
Este análisis comprobará que B y C sean de tipo compatible y que se les pueda aplicar dicho operador
y si B y C son números los sumará, si son cadenas las concatenará y si son conjuntos calculara su unión.
Los compiladores analizan semánticamente los programas para verificar su compatibilidad con las especificaciones semánticas del lenguaje al cual pertenecen
y así poder comprenderlos, para permitir la recepción por parte del procesador de las órdenes cuando ese programa se ejecuta.
Luego de verificar la coherencia semántica,
traduce al lenguaje de la máquina o a una representación portable entre distintos entornos.
Esta fase efectúa la traducción asociada al significado que cada símbolo de la gramática adquiere por aparecer en una producción, asociándole información o atributos, y acciones semánticas a las reglas Gramáticales, que serán código en un lenguaje de programación; para evaluar los atributos y manipular dicha información de las tareas de traducción, mediante los siguientes pasos:
- Análisis léxico del texto fuente.
- Análisis sintáctico de la secuencia de tokens producida por el analizador léxico.
- Construcción del árbol de análisis sintáctico.
- Recorrido del árbol por el analizador semántico ejecutando las acciones semánticas.
Al actuar la semántica y la traducción, los árboles de análisis sintáctico reciben en cada nodo información o atributos, dando lugar a los árboles con adornos, de manera que cada símbolo, se comporta como un registro, cuyos campos son cada uno de sus propios atributos con información semántica, dando lugar al concepto de gramática atribuida.
CÓDIGO INTERMEDIO
Usar lenguaje intermedio permite construir en menor tiempo un compilador para otra máquina y compiladores para otros lenguajes fuente, generando códigos para la misma máquina.
Así, el compilador de C de GNU distribuido con Linux es una versión de una familia de compiladores de C para diferentes máquinas o sistemas operativos: Alpha, AIX, Sun, HP, MS-DOS.
La generación de código intermedio transforma el árbol de análisis sintáctico en una representación en lenguaje intermedio, de código simple para poder luego generar código máquina.

OPTIMIZACIÓN DE CÓDIGO
Abarca los procesos del compilador para generar programas objetos más eficientes, rápido en ejecución, que insuman menos memoria; pero como no podemos asegurar haber conseguido el programa optimo, el termino optimización no es apropiado.
GENERACIÓN DE CÓDIGO
El código intermedio optimizado se traduce a una secuencia de instrucciones en ensamblador o en el código de máquina del procesador que nos interese,
así la sentencia
Z : = X + Y
se convertirá en:
LOAD X ADD Y STORE Z
TABLA DE SIMBOLOS
Es una estructura de datos internos donde el compilador almacena información de objetos que encuentra en el texto fuente, como variables, etiquetas, declaraciones de tipos, etc.
En esta tabla, el compilador puede insertar un nuevo elemento en ella, consultar información relacionada con un símbolo, borrar un elemento, etc.
MANEJO DE ERRORES
Esta tarea del compilador, más solicitada en la etapa de análisis sintáctico y semántico, se dificulta por que muchas veces un error:
- Ocultan otros
- Provoca una avalancha de muchos errores que se solucionan con el primero.
Frente a esto se plantean dos criterios para manejar errores:
- Pararse al detectar el primer error
- Detectar todos los errores de una pasada.
Para diseñar un compilador, la especificación del lenguaje fuente se divide en tres partes:
- ESPECIFICACIÓN LÉXICA:
Mediante expresiones regulares se detallan los componentes léxicos o tokens o palabras del lenguaje. A partir de estas expresiones regulares se construye el analizador léxico del compilador. - ESPECIFICACIÓN SINTÁCTICA:
Detalla la sintaxis o forma o estructura que tendrán los programas en este lenguaje fuente. Tal tarea utiliza una gramática independiente del contexto en notación BNF o un diagrama sintáctico que posteriormente se convierte en una gramática; a partir de la gramática se construye el analizador sintáctico del compilador. - ESPECIFICACIÓN SEMÁNTICA:
Describe el significado de cada construcción sintáctica y las reglas semánticas que deben cumplirse.
El saber y la razón hablan,
la ignorancia y el error gritan..!!
A. Graf

C O M P I L A D O R E S GENERACION DE CÓDIGO INTERMEDIO |
- Cuando una empresa desarrolla un compilador para un lenguaje fuente y un lenguaje objeto determinados, normalmente no es el único compilador que la empresa piensa desarrollar; es más muchos fabricantes de microprocesadores tienen una división de dedicada a desarrollar compiladores para los nuevos chips que construya.
- Cuando el número de lenguaje fuente crece hasta un número grande M, y/o cuando el número de lenguajes objeto también crece hasta un número grande N, es necesario encontrar una técnica para evitar tener que diseñar M x N compiladores.
La solución consiste en utilizar un lenguaje intermedio o una representación intermedia; de esta forma sólo hay que construir M programas que traduzcan de cada lenguaje fuente al lenguaje intermedio (los front ende), y N programas que traduzcan del lenguaje intermedio a cada lenguaje objeto (los back end).
- No existe un único lenguaje intermedio en todos los compiladores, sino que cada empresa que diseña compiladores suele tener su propio lenguaje intermedio.
La utilización de un lenguaje intermedio permite construir en, mucho menos tiempo un compilador para otra máquina y también permite construir compiladores para otros lenguajes fuente generando códigos para la misma máquina.
- Por Ejemplo, el compilador de C de GNU que se distribuye con Linux es una versión de una familia de compiladores de C para diferentes máquinas o sistemas operativos: Alpha, AIX, Sun, HP, MS-DOS, etc..
Además, GNU ha desarrollado un compilador de FORTRAN y otro de Pascal que, al utilizar el mismo lenguaje intermedio, pueden ser portados a todos los sistemas y máquinas en las que y a existe un compilador de C de GNU con relativamente poco esfuerzo.
- La generación de código intermedio transforma un árbol de análisis sintáctico (semántico) en una representación en un lenguaje intermedio, que suele ser código suficientemente sencillo para poder luego generar código máquina.
- Una forma es mediante el llamado código de tres direcciones.
Una sentencia en código de tres direcciones es:
A := B op C, donde
A, B y C son operandos y op es un operador binario.
También permite condiciones simples y saltos.
Esta fase se añade al compilador para conseguir que el programa objeto sea más rápido en ejecución t que necesite menos memoria a la hora de ejecutarse.
El termino optimización no es correcto, ya que nunca podemos asegurar que conseguimos un programa optimo.
Con una buena optimización, el tiempo de ejecución puede llegar a reducirse a la mitad, aunque hay máquinas que pueden no llevar esta etapa y generar directamente código máquina.
Ejemplos de posibles optimizaciones locales:
- cuando hay dos saltos seguidos se puede quedar uno sólo.
- Eliminar expresiones comunes a favor de una sola expresión. Por Ejemplo:
A : = B + C + D E : = B + C + F Se convierte en: T1 : = B + C A : = T1 + D E : = T1 + F
- Optimización de bucles y lazos.
Se trata de sacar de los bucles y lazos las expresiones que sean invariantes dentro de ellos.
Por Ejemplo, dado el siguiente código:REPEAT B : = 1 A := A – B UNTIL A = 0
Se trata de sacar del bucle la asignación B : = 1
El código intermedio optimizado es traducido a una secuencia de instrucciones en ensamblador o en el código de máquina del procesador que nos interese.
Por Ejemplo:
la sentencia A : = B + C se convertirá en:
LOAD B
ADD C
STORE A
Suponiendo que estas instrucciones existan de esta forma en el ordenador de que se trate.
Una conversión tan directa produce generalmente un programa objeto que contiene muchas cargas (load) y almacenamientos (store) redundantes, y que utiliza los recursos de la máquina de forma ineficiente.
Existen técnicas para mejorar esto, pero son complejas.
Por Ejemplo, es tratar de utilizar al máximo los registros de acceso rápido que tenga la máquina.
Así, en el procesador 8086 tenemos los registros internos
AX, BX, CX, DX, etc.
y podemos utilizarlo en vez de direcciones de memoria
Un compilador necesita guardar y usar la información de los objetos que se va encontrando en el texto fuente, como variables, etiquetas, declaraciones de tipos, etc..
Esta información se almacena en una estructura de datos internos conocida como tabla de símbolos.
El compilador debe desarrollar una serie de funciones relativas a la manipulación de esta tabla como insertar un nuevo elemento en ella, consultar la información relacionada con un símbolo, borrar un elemento, etc..
Como se tiene que acceder mucho a la tabla de símbolos los accesos deben ser lo más rápido posible para que la compilación sea eficiente.
Donde más se utiliza es la etapa de análisis sin táctico y semántico, aunque los errores se pueden descubrir en cualquier fase de un compilador.
Es una tarea difícil, porque:
- A veces unos errores ocultan otros
- A veces un error provoca una avalancha de muchos errores que se solucionan con el primero.
Es conveniente un buen manejo de errores, y que el compilador detecte todos los errores que tiene el programa y no se para en el primero que encuentre.
Hay dos criterios a seguir a la hora de manejar errores:
- Detectar todos los errores de una pasada.
Pararse a detectar el primer error
En el caso de un compilador interactivo (dentro de un entorno de desarrollo integrado, como Turbo Pascal o Borland C++) no importa que se pare en el primer error detectado, debido a la rapidez y facilidad para la corrección de errores.
Cuando se va diseñar un compilador, puesto que se trata de un traductor entre dos lenguajes, es necesario especificar el lenguaje fuente y el lenguaje objeto, así como el sistema operativo sobre el que va a funcionar el compilador y el lenguaje utilizado para construir el compilador.
Existen algunas herramientas formales para especificar los lenguajes objetos, pero no existe ninguna herramienta cuyo uso sea extendido.
La especificación del lenguaje fuente se divide en tres partes:
- Especificación sintética:
Se detalla la forma o estructura (la sintaxis) que tendrán los programas en este lenguaje fuente.
Para esta tarea se utiliza una gramática independiente del contexto en notación BNF o un diagrama sintáctico que posteriormente se convierte en una gramática; a partir de la gramática se construye el analizador sintáctico del compilador. - Especificación semántica.:
Se describe el significado de cada construcción sintáctica y las reglas semánticas que deben cumplirse, aunque existen notaciones formales para especificar la semántica del lenguaje, normalmente se especifica con palabras (lenguaje natural).
Algunas veces es posible recoger en la especificación sintáctica algunas partes (restricciones, asociatividad, y precedencia, etc.) de la especificación semántica.
El analizador semántico y el generador de código intermedio se construye apartir de la especificación semántica.
Especificación léxica:
Se especifican los componentes léxicos (tokens) o palabras del lenguaje para ello se utilizan expresiones regulares.
A partir de estas expresiones regulares se construye el analizador léxico del compilador.
La importancia practica de lenguaje en la informática se manifiesta principalmente en el uso cotidiano que hace el profesional informático de compiladores e interpretes, consustancial al la gestión y programación de los sistemas informáticos.
Así pues, un conocimiento acerca del funcionamiento interno de estas herramientas básicas resulta fundamental. Pero los conocimientos adquiridos en su estudio encuentren aplicación fuera del campo de la compilación.
Es probable que ocas personas realice o mantenga un compilador para un lenguaje de programación, pero mucha gente puede obtener provecho del uso de un gran número de sus técnicas para el diseño de software en general.
En informática la aplicación de técnicas en COMPILADORES e INTÉRPRETES se puede citar:
- Tratamiento de ficheros de texto con información estructurada.
Lenguaje como Perl y TEL, o comandos como el sed o egrep de UNIX,
incorpora tratamiento de expresiones regulares para la detección y/o modificación de patrones sin texto. - Procesadores de texto.
Procesadores como vi o Emacs incorporan también la posibilidad de efectuar búsquedas y sustituciones mediante expresiones regulares.
Existen también procesadores (entre ellos los Emacs) capaces de analizar y tratar ficheros de texto de organización compleja. - Diseño e interpretación
De lenguaje para formateo y texto y descripción de gráficos.
Sistema de formateo de texto (como el HTML o el TEX)
o para la especificación de tablas (tbl), ecuaciones (eqn), gráficos (postscript), etc. requieren sofisticados microprocesadores. - Gestión de base de datos.
Las técnicas que estamos considerando pueden explotarse tanto en la exploración y proceso de ficheros de información como en la realización de la interfase de usuario. - Traducción de formato de fichero.
- Calculo simbólico.
- Reconocimiento de formas.
Las técnicas de análisis sintáctico son ampliamente utilizadas en la detección de patrones en texto, el reconocimiento automático del habla o la visión por computador.

C O M P I L A D O R E S ANALISIS L É X I C O |
Es, por otra parte, el único que gestiona el fichero de entrada.
Es la parte del compilador que lee los caracteres del programa fuente y que construye unos símbolos intermedios (elementos léxicos que llamaremos “tokens”) que serán posteriormente utilizados por el analizador sintáctico como entradas.
El analizador sintáctico debe obtener una representación de la estructura (sintaxis) del programa fuente. Para realizar esta tarea debería concentrarse solamente en la estructura y no en otros aspectos menos importantes, como los espacios construidos con una gramática que genere los programas carácter no son útiles para construir una traducción.
¿Por qué separar el análisis léxico del sintáctico?
- El diseño de las partes posteriores dedicadas al análisis queda simplificado.
- Con fases separadas, se pueden aplicar técnicas específicas y diferenciadas para cada fase, que son más eficientes en sus respectivos dominios.
- Se facilita la portabilidad. Si se quiere cambiar alguna característica del alfabeto del lenguaje (por Ejemplo para adaptarlo a determinados símbolos propios de máquinas distintas) sólo tenemos que cambiar el analizador léxico.
Si tomamos por Ejemplo las expresiones “6 – 2 * 30 / 7” y “6 – 2 * 30 / 7”,
podemos comprobar que la estructura de ambas expresiones es equivalente,
sin embargo, los caracteres que componen ambas cadenas no son los mismos.
Si tuviéramos que trabajar directamente con los caracteres estaríamos dificultando la tarea de obtener la misma representación para ambas cadenas.
Si consideramos además la cadena “8 – 2 * 3 / 5”, la estructura de esta cadena es de nuevo la misma que la de las cadenas anteriores, lo único que cambia son los valores concretos de los números.
Por estos motivos (y también por eficiencia), el procesamiento de los caracteres se deja en mano del analizador léxico que entregará a las sucesivas etapas del compilador los componentes léxicos (tokens) significativos.
Donde cada token ha sido representado por un par en el que la primera componente de cada par es el tipo de token y la segunda componente es el lexema (el valor concreto de ese token).
La tercera cadena del Ejemplo anterior tendría la misma estructura que las otras dos, pero con distintos valores de los lexemas.
En definitiva, el análisis léxico agrupará los caracteres de la entrada por categorías léxicas, establecidas por la especificación léxica del lenguaje fuente como veremos más adelante.
Esta especificación también establecerá el alfabeto con el que se escriben los programas válidos en el lenguaje fuente y, por tanto, el analizador léxico también deberá rechazar cualquier texto en el que aparezcan caracteres ilegales (no recogidos en ese alfabeto) o combinaciones ilegales (no permitidas por las especificaciones léxicas) de caracteres del alfabeto.
Los componentes léxicos se especifican mediante expresiones regulares que generan lenguajes regulares, más sencillos de reconocer que los lenguajes independientes del contexto, y permiten hacer un análisis más rápido.
Además, una gramática que represente la sintaxis de un lenguaje de alto nivel carácter a carácter sería mucho más compleja (para implementar un proceso de traducción a partir de ella) que otra que representase la misma sintaxis en función de sus componentes léxicos.
2.2 ERRORES LEXICOS
Pocos son los errores característicos de esta etapa, pues el compilador tiene todavía una visión muy local del programa.
Por Ejemplo, si el analizador léxico encuentra y aísla la cadena “While” creerá que es un identificador, cuando posiblemente se tratara de un while mal escrito y no será él el que informe del error, sino que lo harán sucesivas etapas del análisis del texto.
Los errores que típicamente detecta el analizador léxico son:
- Utilizar caracteres que no pertenecen al alfabeto del lenguaje (por Ej.: “ñ” o”?”).
- Se encuentra una cadena que no coincide con ninguno de los patrones de los tokens posibles (por Ej.: “123dfxr”o “123.456.789”si la especificación léxica no los permite).
Cuando el analizador léxico encuentra un error, lo habitual es parar su ejecución e informar,
pero hay una serie de posibles acciones por su parte para anotar los errores, recuperarse de ellos y seguir trabajando:
- Ignorar los caracteres no válidos hasta formar un token según los patrones dados;
- Borrar los caracteres extraños;
- Insertar un carácter que pudiera faltar;
- Reemplazar un carácter presuntamente incorrecto por uno correcto;
- Conmutar las posiciones de dos caracteres adyacentes.
Estas transformaciones se realizan sobre el prefijo de entrada que no concuerda con el patrón de ningún token, intentando conseguir un lexema válido.
No obstante, todas son complicadas de llevar a cabo y peligrosas por lo equivocadas que pueden resultar para el resto del análisis.
2.3 FUNCIONAMIENTO
DEL ANALIZADOR LEXICO
La principal función del analizador léxico es procesar la cadena de caracteres y devolver pares (token, lexema). Debe funcionar como una subrutina del analizador sintáctico.
Operaciones que realiza el analizador léxico:
- Proceso léxico del programa fuente: identificador de tokens y de sus lexemas que deberán entregar al analizador sintáctico y (puede que) interaccionar con la tabla de símbolos.
- Maneja el fichero del programa fuente; es decir: abrirlo, leer sus caracteres y cerrarlo.
También debería ser capaz de gestionar posibles errores de lectura. - Ignorar los comentarios y, en los lenguajes de formato libre, ignora los separadores (espacios en blanco, tabuladores, retornos de carro, etc.).
- Cuando se produzca una situación de error será el analizador léxico el que sitúe el error en el programa fuente (tal línea, tal posición).
Lleva la cuenta de las líneas procesadas. - Proceso de macros, definiciones, constantes y órdenes de inclusión de otros ficheros.
Cada vez que el analizador sintáctico llame al léxico éste debe leer caracteres desde donde se quedó en la anterior llamada hasta conseguir completar un nuevo token, y en ese momento debe devolver el par (token, lexema).
Cuando el analizador léxico intenta reconocer algunos tipos de tokens como los identificadores o los números se produce una circunstancia especial:
- el analizador léxico debe leer caracteres hasta que lea uno que no pertenece a la categoría del token que está leyendo; ese último carácter (que no tiene por qué ser un espacio en blanco) no puede perderse,
- y debe devolverse el buffer de entrada para ser leído en primer lugar la próxima vez que se llame al analizador léxico.
Ejemplo
En la cadena:
“Grande / 307 ??=”
marcamos las posiciones a las que tiene que llegar el analizador léxico
para decidir qué tokens ha reconocido.
Grande / 307 ??=
Como se puede observar, para el caso del identificador “Grande”,
ha tenido que ir una posición más allá del final del mismo, pues sólo allí, al encontrar el espacio en blanco puede que el nombre del identificador ha concluido.
Para encontrar el símbolo “/” basta con ponerse sobre él y verlo si consideramos que no es prefijo de ninguno otro (para este lenguaje imaginario).
Para el número “307” sucede lo mismo que con el identificador:
hay que llegar hasta un carácter que no sea un número para saber que el número ha terminado.
Este símbolo es este caso es el signo”?” de “?=” (mayor o igual que).
Después, para reconocer este nuevo token el léxico avanzará para ver si es el “=” lo que sigue al “?”.
Como sí que lo es y suponemos que “=” no es prefijo de ningún otro,
el analizador devolverá el token “mayor o igual”,
si no hubiera aparecido el igual al avanzar,
hubiera tenido que retroceder una posición
y devolver el token “mayor”.
El analizador léxico debe intentar leer siempre el token más largo posible.
Puede ocurrir que haya leído ya un token correcto y al intentar leer un token más largo no sea posible;
en este caso no se debe producir un error,
sino que el analizador léxico debe devolver al token correcto
y debe retroceder en el buffer de entrada hasta el final de ese token.
Ejemplo
Si el operador “!=” (distinto)
pertenece al lenguaje pero el carácter “!” No,
cuando aparezca en la entrada este carácter,
el analizador debe leer el siguiente carácter;
si es un “=”, deberá el token correspondiente al operador distinto,
pero si no es un “=”, debe producir un error léxico
`puesto que el carácter “!” por si solo no pertenece al lenguaje.
2.4 ESPECIFICACIONES
DE UN ANLIZADOR LEXICO
Definición de términos comunes en esta fase:
- Tokens:
son los símbolos terminales de cada gramática
(por Ejemplo: palabras reservadas, identificadores, signos de puntuación, constantes numéricas, operadores, cadenas de caracteres, etc.).
Es posible, dependiendo del lenguaje, que varios signos formen un solo token
(“: =”, “= =”, “+ =”, “???”, etc.). - Patrón:
expresión regular que define el conjunto de cadenas que puede representar a cada uno de los tokens. - Lexema:
secuencia de caracteres del código fuente que concuerda con el patrón de un token. Es decir, cuando analizamos el texto fuente y encontramos una cadena de caracteres que representan un token determinado diremos que esa cadena es un lexema. - Atributos:
el análisis léxico debe proporcionar información adicional sobre los tokens en sus atributos asociados.
El número de atributos depende de cada token.
En la práctica, se puede considerar que los tokens tiene un único atributo, un registro que contiene toda la información propia de cada caso (por Ejemplo, lexema, tipo de token y línea y columna en la que fue encontrado).
Lo normal es que toda esa información se entregue a los analizadores sintácticos y semánticos para que la usen como convenga.
Cuando el analizador léxico encuentra un lexema devuelve como información a qué token pertenece y todo lo que sabe de él, incluido el propio lexema.
En el último caso, se supone que esa palabra pertenece a un lenguaje en el que mayúsculas y minúsculas son equivalentes.
Para especificar correctamente el funcionamiento de una analizador léxico se debe utilizar una máquina de estados, llamada diagrama de transición (DT), muy parecida a un autómata finito determinista, con las siguientes diferencias:
- Un AFD sólo dice se la cadena de caracteres pertenece al lenguaje o no; un DT debe funcionar como un analizador léxico; es decir, debe leer caracteres hasta que complete un token, y en ese momento debe retornar, (en los estados de aceptación) el token que ha leído y dejar el buffer de entrada preparado para la siguiente llamada.
- Un DT no puede tener estados de absorción (para cadenas incorrectas en AFDs) ni de error (se considerará que las entradas para las que no hay una transición desde cada estado son error).
- De los estados de aceptación de un DT no deben salir transiciones.
- En el caso de las tiras no especificadas, necesitamos otro estado a que ir cuando se lea un carácter que no puede formar parte del patrón. En este último estado (al que se llega con la transición especial otro) se debe devolver al buffer de entrada el carácter leído (que puede ser parte del siguiente token), lo cual se indica marcando el estado con un asterisco, y se debe retornar el token correspondiente a ese estado de aceptación. Por Ejemplo, para reconocer números enteros, con un AFD son necesarios solamente dos estados; con un DT necesitamos ese otro estado al que ir cuando se lea un carácter que no que no pueda formar parte del número.
En el caso más general, se suelen utilizar estos diagramas de transiciones para conocer los tokens de entrada, construidos a partir de sus patrones correspondientes, expresados mediante las respectivas expresiones regulares.
Estos autómatas se combinan en una máquina única que, partiendo de un único estado inicial, sigue un recorrido u otro por los estados hasta llegar a alguno de los estados de aceptación.
En función de en cual se detenga devolverá un token u otro.
Si no llega a un estado de aceptación o recibe una entrada que no le permite hacer una transición a otro estado, entonces dará error.
Ejemplo
Ejemplo de reconocedor de números enteros sin signo mediante la expresión regular [0-9].
El AFD sería:
y el DT:
Como se observa, en el DT surge un nuevo estado, que es realmente el de aceptación y que está marcado con un asterisco que indica que se llega a él leyendo un carácter a la entrada.
La transición a ese estado se hace mediante la entrada otro que significa cualquier otro carácter del alfabeto del lenguaje que no esté en el rango [0-9].
Si durante el recorrido del autómata se produce una transición no autorizada o la tira de entrada finaliza en un estado no de aceptación, el analizador informará del error.
Este tipo de máquinas es útil para lenguajes con grandes conjuntos de elementos léxicos distintos y de las matrices de transición resultantes tienen grandes zonas vacías que conviene comprimir y resumir mediante algoritmos adecuados.
Cuando los lenguajes son poco extensos es mejor redactar los analizadores “a mano”, tratando de tomar decisiones adecuadas en función de los caracteres que van apareciendo en la entrada (ver apartado de implementación, más adelante).
El analizador suele tener unos subprogramas auxiliares encargados de gestionar el buffer (técnicas de doble buffer, saltos de línea, < EOF < , etc.) y de ir devolviendo caracteres al buffer de entrada cada vez que el procedimiento de reconocimiento y aislamiento de tokens lo requiere.
Identificación de palabras reservadas:
Las palabras reservadas son aquellas que los lenguajes de programación reservan para usos particulares.
El problema que surge es: ¿cómo reconocer las palabras reservadas si responden al mismo patrón que los identificadores, pero son tokens diferentes al token “identificador”?.
Existen dos enfoque para resolver este problema:
1) saltándose el formalismo para buscar una solución práctica (factible si se implementa el A.L. “a mano”);
2) integrando los DT (más complicado pero necesario si usamos programas de conversión automática de especificaciones en analizadores).
La primera solución citada consiste que las palabras reservadas son en principio identificadores, y entonces leer letras y dígitos hasta completar un identificador, e inmediatamente antes de retomar el token identificador, comparar el lexema leído con una lista de las palabras reservadas, para ver si coinciden con alguna de ellas.
En definitiva, se procede normalmente tratando las palabras reservadas como lexemas particulares del patrón del identificador, y cuando se encuentra una cadena que responde a dicho patrón, se analiza si es una palabra reservada o un identificador.
Una posible solución para ello es, en el A.L.:
- Primero inicializar la tabla de símbolos con todas las palabras reservadas (lo normal es hacerlo por orden alfabético para facilitar la posterior búsqueda y acceso).
- Cuando encuentre un identificador se irá a mirar la tabla de símbolos.
- ==> Si lo encuentra en la zona reservada para ellas ENTONCES es una palabra reservada
- ==> SI NO, será un identificador, que, como tal, será añadido a la tabla de símbolos.
Ejemplo
Si se encuentra el identificador “Cont.” en la entrada, antes de que el A.L. devuelva el token identificador deberá comprobar si se trata de una palabra reservada. Si el número de palabras reservadas es muy grande lo mejor es tenerlas almacenadas desde el principio de la compilación en la tabla de símbolos, para ver si allí ya se encuentra definida esa cadena como tal. Aquí hemos supuesto que no es así y “Cont.” queda registrado como un identificador.
Tabla de Símbolos do Pal. Reservada end Pal. Reservada for Pal. Reservada while Pal. Reservada ... .... cont. Identificador
La disposición de una tabla ordenada con las palabras reservadas es útil cuando el número de estas es grande.
Cuando el lenguaje tiene sólo unas pocas puede ser más práctico el realizar la identificación “directamente”, mediante una serie de ifs que comparen con las cadenas correspondientes a esas palabras.
Cuando la detección de palabras reservadas se hace, en cambio, formalmente, entonces los patrones de la especificación léxica del lenguaje tendrán su correspondencia en el diagrama de transiciones global a partir del cual se implementará el analizador léxico.
Las especificaciones léxicas de las palabras reservadas, como tira especificadas que son, constarán de concatenaciones de caracteres y pueden ser siempre prefijos de identificadores (como por Ejemplo “do” –palabra reservada- y “dos” –identificador-).
Cuando en la especificación léxica del lenguaje coexisten expresiones regulares de tiras no específicas como los identificadores con las de específicas como las palabras reservadas, hay que llevar más cuidado porque cualquiera de las palabras reservadas puede ser un prefijo de un identificador válido. Esto motiva que los subautómatas que reconocen las palabras deben estar comunicados con el de los identificadores (ver Ejemplo más abajo).
Por otra parte, cuando un elemento léxico es prefijo de otro y ambos son tiras específicas, aparecerán estados de aceptación que partirán de estados intermedios
Ejemplo
Constrúyase un diagrama de transiciones para el reconocimiento de identificadores, números enteros sin signo y las palabras reservadas “do” y “done”.
Notación:
d = dígito; l = letra; t = otro; f = otro alfanumérico (dígito o letra); a n = ir al estado n.
Como se observa en este diagrama de transiciones, todos los estados de aceptación están marcados con asterisco, por lo que siempre que devolver el último carácter leído al buffer de entrada.
Esto es debido, en este Ejemplo a que todos los tokens son bien unos prefijos de otros (do?done?identificador) o bien son tiras no especificadas (entero e identificador).
Ejemplo
Constrúyase un diagrama de transiciones para el reconocimiento de números enteros con signo negativo o sin signo (ER: (-???*?d+) y los operadores suma (“+”) y doble incremento (“+++”).
Notación: d=dígito; t=otro.
Obsérvese que el estado de aceptación del token “doble incremento” no lleva asterisco por ser una tira específica y no ser prefijo de ninguna otra,
y por tanto no necesita la lectura del siguiente carácter y el retroceso.
Si que lo llevan los estados de aceptación del token “suma” a pesar de ser específicas, pues son prefijos del “doble incremento”.
Además, uno de ellos lleva dos asteriscos, indicando que si se llega a ese estado hay que retornar el token “suma” pero hay que devolver dos caracteres al buffer de entrada.
2.5 IMPLEMENTACION DE
ANALIZADORES LEXICOS
existen distintas posibilidades para de crear un analizador léxico,
las tres más generales son:
- Usar un generador automático de analizadores léxicos, como el LEX: su entrada es un código fuente con la especificación de las expresiones regulares de los patrones que representan a los token del lenguaje, y las acciones a tomar cuando los detecte.
- Ventaja: comodidad y rapidez en el desarrollo.
- Inconveniente: ineficiencia del analizador resultante y complicado mantenimiento de código generador.
- Escribir el AL en un lenguaje de alto nivel de uso general utilizando sus funciones de E/S.
- Ventaja: más eficiente.
- Inconveniente: hay que hacerlo todo a mano.
- Hacerlo en lenguaje ensamblador.
- Ventaja: máxima eficiencia.
- Inconveniente: muy complicado de desarrollar.
Como se ha indicado, la forma más cómoda de implementar un analizador léxico es con un generador automático de analizadores léxicos, como lex, si bien no es la forma más eficiente. Si se opta por hacerlo “a mano”, se puede hacer de varias maneras: implementando el diagrama de transiciones simulando las transiciones entre estados o bien se pueden implementar “directamente”, usando estructuras de selección múltiple (switch en C, case en Pascal, etc.) para, según cual sea el primer carácter del tolken, leer caracteres hasta completar el token. Por supuesto, con esta técnica también es necesario al buffer de entrada.
Por otro lado, lo normal cuando se construye un A.L. es establecer criterios para dar más prioridad a unos tokens que a otros. Criterios:
* Dar prioridad al token para el que encontramos el lexema más largo. Por ej: “DO” / “DOT”, el generador se quedaría con el más largo (“DOT”) como identificador (otro Ejemplo: “>”" y “>=” se debe quedar con el segundo).
Si el lexema es el mismo que se puede asociar a dos tokens (patrones), estos patrones estarán definidos en un orden, así se asociará al que esté primero.

C O M P I L A D O R E S ANALISIS S I N T Á C T I C O |
Para ello, el analizador sintáctico (A.S.) comprueba que el orden en que el analizador léxico le va entregando los tokens es válido. Si esto es así significar que la sucesión de símbolos que representan dichos tokens puede ser generada por la gramática correspondiente al lenguaje del código fuente.
A partir de ese recorrido el analizador sintáctico debe construir una representación intermedia de ese programa fuente: un árbol sintáctico abstracto o bien un programa en un lenguaje intermedio; por este motivo, es muy importante que la gramática esté bien diseñada, e incluso es frecuente rediseñar la gramática original para facilitar la tarea de obtener la representación intermedia mediante un analizador sintáctico concreto.
Ejemplo
Los árboles sintácticos abstractos son materializaciones de los árboles de análisis sintáctico en los que se implementan los nodos de éstos, siendo el nodo padre el operador involucrado en cada instrucción y los hijos sus operandos.
Por otra parte, las representaciones intermedias son lenguajes en los que se han eliminado los conceptos de mayor abstracción de los lenguajes de programación de alto nivel.
Sea la instrucción “a=b+c-d”. A continuación se muestra su representación mediante ambos esquemas citados.
Árbol sintáctico abstracto
Lenguaje intermedio
Sumar b c t1 Restar t1 d t2 Asignar t2 a
El A.S. constituye el esqueleto principal del compilador.
Habitualmente el analizador léxico se implementa como una rutina dentro del sintáctico, al que devuelve el siguiente tokens que encuentre en el buffer de entrada cada vez que éste se lo pide.
Así mismo, gran parte del resto de etapas de un programa traductor están integradas de una u otra forma en el analizador sintáctico.
Principalmente hay dos opciones para implementar un parser:
- “a mano”, utilizando una serie de técnicas que se describirán en los siguientes temas;
- utilizando un generador de analizadores sintácticos (por Ej. el YACC).
Como siempre, ambos enfoques tienen ventajas e inconvenientes, muy similares al caso de los analizadores léxicos (para el segundo caso el inconveniente de la ineficiencia y la ventaja de la sencillez, y viceversa para el primero).
En este tema nos centramos técnicas para implementar a mano parsers para determinados tipos de gramáticas.
3.2 NOTACIÓN EBNF
EBNF son las siglas de Extended Backus-Naur Form.
La idea surgió como herramienta para reducir el número de producciones en las gramáticas,
Para ello se añaden unas notaciones adicionales a las ya contenidas en la notación BNF.
- Alternativas de una regla:
Como un mismo símbolo auxiliar puede definirse como varios símbolos, utilizamos una única producción utilizando el símbolo '|' para separar las distintas posibilidades que definen al no terminal de la izquierda.Ejemplo: si A --> a A --> b A --> cestas tres producciones las resumimos en una equivalente:
A -->a | b | cOtro:
--> | - Llaves: { }, lo que aparece entre llaves se repite de cero a n veces.
Ejemplos:
--> {, } --> { } - Llaves con repetición especificada: { }xy, lo que aparece entre llaves se repite un número de veces comprendido entre x e y.
Ejemplo:
tren con 3, 4 ó 5 vagones:--> { }35 - Corchetes: [ ], lo que está entre los corchetes puede o no aparecer. Es un caso particular de 3.-, pues es equivalente a { }o1
Ejemplo:
Sentencia IF completa en Pascal:IF
THEN [ELSE ] - Llaves: { }, lo que aparece entre llaves se repite de cero a n veces.

para ANALISIS LENGUAJES de PROGRAMACÍON |
Por otro lado, es evidente que la especificación sintáctica de un lenguaje debe ser finita.
El concepto que hace compatible las dos afirmaciones anteriores es el de recursividad. Ésta nos permite definir sentencias complicadas con un número pequeño de sencillas reglas de producción.
Ejemplo
Supongamos que queremos expresar la estructura de un tren formado por una locomotora y un número cualquiera de vagones detrás. Si lo hiciéramos de esta forma:
tren --> locomotora
tren --> locomotora vagón
tren --> locomotora vagón vagón
Necesitaríamos infinitas reglas de derivación (una por cada número de vagones posibles en el tren).
Para expresar lo mismo con un par de sentencias podemos utilizar la recursividad de la siguiente manera:
1°) definimos la regla base (no recursiva), la cual define el concepto elemental de partida y que en este caso sería: tren --> locomotora
2°) definimos una o más reglas recursivas que permiten el crecimiento ilimitado de la estructura partiendo del concepto elemental anterior. En este caso una nos basta:
tren --> tren vagón
y con esto nos ahorramos la utilización de muchas más reglas.
Estructura de la recursividad:
1. Regla no recursiva que se define como caso base.
2. Una o más reglas recursivas que permiten el crecimiento a partir del caso base.
Definición:
Una gramática se dice que es recursiva, si podemos derivar una tira en la que nos vuelve a aparecer el símbolo no terminal que aparece en la parte izquierda de la regla de derivación.
A => ?A?
Unos casos especiales de recursividades son aquellos en los que aparecen derivaciones como A => ?? o A => ?A y se denominan recursividad izquierda y derecha, respectivamente.
Un no terminal A se dice que es recursivo si a partir de A se puede derivar una forma sentencial en aparece él mismo en la parte derecha.
3.3.2 AMBIGÜEDAD
Una gramática es ambigua si el lenguaje que define contiene alguna sentencia que tenga más de un único árbol de análisis sintáctico. Es decir, si se pueden construir más de un árbol sintáctico quiere decir que esa sentencia puede “querer decir” cosas diferentes (tiene más de una interpretación). Una gramática es no ambigua cuando cualquier tira del lenguaje que representa, tiene un único árbol sintáctico.
Como veremos más adelante, no es posible construir ana1izadores sintácticos eficientes para gramáticas ambiguas y, lo que es peor, al poderse obtener más de un árbol sintáctico para la misma cadena de entradas, es complicado conseguir en todos los casos la misma representación intermedia. Por estos motivos debemos evitar diseñar gramáticas ambiguas para los lenguajes de programación; aunque no disponemos de técnicas para saber a priori si una gramática es ambigua o no, si ponemos ciertas restricciones a la gramática estaremos en condiciones de afirmar que no es ambigua.
La única forma de saber que una gramática es ambigua es encontrando una cadena con dos o más árboles sintácticos distintos (o dos derivaciones por la izquierda). Las gramáticas que vamos a utilizar normalmente generan lenguajes infinitos, por tanto no es posible encontrar en un tiempo finito esa cadena con dos o más árboles sintácticos. Sin embargo, si la gramática tiene alguna de las siguientes características, es sencillo encontrar una cadena con dos o más árboles:
ASOCIATIVIDAD Y PRECEDENCIA
DE LOS OPERADORES
Asociatividad
Define como se operan tres o más operandos; se dice que la asociatividad de un operador ‘#’ es por la izquierda si aparecen tres o más operandos que se evaluando izquierda a derecha:
primero se evalúan los dos operandos de más a la izquierda, y el resultado de esa operación se opera con el siguiente operando por la izquierda, y así sucesivamente.
Si la asociatividad del operador es por la derecha, los operandos se evalúan de derecha a izquierda.
En los lenguajes de programación imperativos más utilizados, la asociatividad de la mayoría de los operadores y en particular la de los operadores aritméticos es por la izquierda.
Ejemplo
Si la asociatividad del operador ‘#’ es por la izquierda, la expresión ‘2 # a # 7.5’ se evalúa operando primero el ‘2’ con la variable ‘a’, y operando después el resultado con ‘7.5’.
si la asociatividad fuera por la derecha, primero se operarían la variable ‘a’ con el ‘7.5’ y después se operaría el ‘2’ con el resultado de esa operación.
Ejemplo
En Fortran existen cinco operadores aritméticos:
suma (“+”), resta (“-”), multiplicación (“*”), división (“/”) y exponenciación (“**”).
Los cuatro primeros son asociativos por la izquierda,
mientras que el último lo es por la derecha:
* A / B / C se evalúa como A / B y el resultado se divide por C *
X ** Y ** Z se evalúa como Y ** Z y X se eleva al resultado
Cuando la asociatividad del operador es por la izquierda, la regla sintáctica en la que interviene dicho operador debe ser recursiva por la izquierda, y cuando es por la derecha, la regla en la que interviene debe tener recursión por la derecha.
Precedencia
Especifica el orden relativo de cada operador con respecto a los demás operadores; si un operador ‘#’ tiene mayor precedencia que otro operador ‘%’, cuando en una expresión aparezcan los dos operadores, se debe evaluar primero el operador con mayor precedencia.
Ejemplo
Si aparece una expresión como ‘2 % 3 # 4’, al tener el operador ‘#’ mayor precedencia, primero se operarían el ‘3’ y el ‘4’, y después se operaría el ‘2’ con el resultado de esa operación.
En la mayoría de los lenguajes de programación los operadores multiplicativos tienen mayor precedencia que los aditivos, se evalúan las multiplicaciones y divisiones de izquierda a derecha antes que las sumas y restas.
La forma de reflejar la precedencia de los operadores aritméticos en una gramática es bastante sencilla. Es necesario utilizar una variable en la gramática por cada operador de distinta precedencia. Cuanto más “cerca” este la producción de la del símbolo inicial, menor será la precedencia del operador involucrado.
Parentización
Se utilizan los paréntesis (que son operadores especiales que siempre tienen la máxima precedencia) para agrupar los operadores según la conveniencia del programador y sortear las precedencias y asociatividades definidas en el lenguaje.
Para incluirlos en la gramática, se añade una variable que produzca expresiones entre paréntesis los operandos a la mayor distancia posible del símbolo inicial.
Ejemplo
Suponiendo los operadores +, -, con asociatividad por la izquierda y los operadores *, / con asociatividad por la derecha.
Sean para los dos tipos de operadores la precedencia habitual en los lenguajes de programación y los paréntesis tienen la máxima precedencia. La gramática que genera las expresiones con estos operadores y además recoge la asociatividad y la precedencia es la siguiente:
Esta gramática refleja la precedencia y asociatividad de los operadores.
Esto es importante puesto que en la mayoría de los lenguajes objeto los operadores no tienen precedencia o asociatividad. Si el árbol sináptico mantiene correctamente agrupados los operandos de dos en dos será más sencillo evaluar la expresión y traducirla a un lenguaje objeto típico.
TIPOS DE
ANÁLISIS SINTÁCTICO
Los algoritmos de Análisis Sintáctico general para gramáticas independientes del contexto tienen un coste demasiado elevado para un compilador.
Desde el punto de vista de la teoría de Análisis Sintáctico, hay dos estrategias para construir el árbol sintáctico:
* Análisis descendente:
partimos de la raíz de árbol (donde estará situado el axioma o símbolo inicial de la gramática) y se van aplicando reglas por la izquierda, de tal forma se obtiene una derivación por la izquierda de la cadena de entrada. Para decidir que regla aplicar se lee un token de la entrada.
Recorriendo el árbol en profundidad de izquierda a derecha, encontraremos en las hojas los tokens, que nos devuelve el A.L. en ese mismo orden.
* Análisis ascendente:
partiendo de la cadena de entrada se construye el árbol empezando por las hojas y se van creando nodos intermedios hasta llegar a la raíz; construyendo así al árbol de abajo hacia arriba. El recorrido se hará desde las hojas a la raíz. El orden en el que se van encontrando las producciones corresponde a la inversa de una derivación por la derecha.
Las dos estrategias recorren la cadena de entrada de izquierda a derecha una sola vez, y necesitan un análisis eficiente para que la gramática no sea ambigua.
Ejemplo
Ambos tipos de análisis son eficientes pero no son capaces de trabajar con todo tipo de gramáticas.
Algunas gramáticas adecuadas para estos tipos de análisis son muy convenientes para describir la mayoría de lso lenguajes de programación, por Ejemplo los siguientes:
* Análisis LL(n)
* Análisis LR(n)
Donde
L Left to Right: la secuencia de tokens de entrada se analiza de izquierda a derecha.
L Left-most (R = Right-most): utiliza las derivaciones más a la izquierda (a la derecha).
n: es en número de símbolos de entrada que es necesario conocer en cada momento para poder hacer el análisis.
Una gramática LL(2) es aquella cuyas cadenas son analizadas de izquerda a derecha y para las que es necesario mirar dos tokens para saber que derivación tomar para el no terminal más a la izquierda en el árbol de análisis. Conn estos tipos de análisis podemos implementar un analizador para cualquier gramática de contexto libre. <

C O M P I L A D O R E S ANÁLISIS SEMÁNTICO |
Los compiladores analizan semánticamente los programas para ver si son compatibles con las especificaciones semánticas del lenguaje al cual pertenecen y así poder comprenderlos, teniendo claro que la comprensión para la máquina representa la recepción por parte del procesador de una serie de órdenes cuando ese programa se ejecuta.
Cuando el compilador verifica la coherencia semántica lo traduce al lenguaje de la máquina o a una representación que permita una mayor portabilidad entre distintos ambientes.
Es la fase de análisis semántico la que lleva a cabo acciones de traducción asociada al significado que cada símbolo de la gramática adquiere por aparecer en una producción u otra. Para que los símbolos puedan adquirir significados, se les asociará información (atributos) y a las reglas Gramáticales, acciones semánticas, que serán código en un lenguaje de programación; y cuya misión es evaluar los atributos y manipular dicha información para llevar a cabo las tareas de traducción.
Para el análisis semántico se deben haber llevado a cabo los siguientes pasos:
- * Análisis léxico del texto fuente.
- * Análisis sintáctico de la secuencia de tokens producida por el analizador léxico.
- * Construcción del árbol de análisis sintáctico.
- * Recorrido del árbol por el analizador semántico ejecutando las acciones semánticas.
La cadena de entrada se analiza sintácticamente, construyendo su árbol de análisis sintáctico, y el recorrido del árbol lleva implícito la evaluación en sus nodos del resultado de ejecutar las reglas de traducción.
Como resultado se obtendrá la traducción a lenguaje objeto de la cadena de elementos léxicos que fue suministrada por el analizador léxico y supervisada en su orden por el sintáctico.
El concepto de gramática con atributos y la inclusión de las acciones semánticas lleva a que conforme se va haciendo el análisis se vayan evaluando las acciones semánticas.
Los analizadores sintácticos y semánticos se implementarán como un único subprograma, imposible de disociar por un programador no experto en el diseño de compiladores.
Veremos que estas operaciones de traducción son propias de cada nodo del árbol. El comportamiento de la información siempre es el mismo en cada regla.
CONCEPTOS Y TIPOS DE ATRIBUTOS
Cuando la semántica y la traducción entran en juego, a los árboles de análisis sintáctico se les añade información en cada nodo.
Estos árboles reciben el nombre de “árboles con adornos”.
Para que esa información pueda viajar atrtavés del árbol hace falta un “almacenes”, que se llaman atributos.
Cada símbolo tiene sus propios atributos en los que almacena la información semántica.
La existencia de atributos para los símbolos de la gramática, conduce al concepto de gramática atribuida. Cada símbolo puede contemplarse como un registro, cada uno de cuyos campos es un atributo distinto:
A = (A.tipo, A.valor, A.dirección, …)
Cualquier producción de la gramática tiene asociado un árbol sintáctico:
Si A --> a1 a2 … an su árbol será: A
La evaluación de los atributos se realiza mediante operaciones que reciben el nombre de reglas o acciones semánticas.
Estas se realizan sobre los valores de los atributos de los símbolos de esa misma regla (sub-árbol):
A.a = f(a1.ai, a2.ai, …, an.an, A.ai)
Los atributos mantienen este carácter a lo largo de toda la gramática. Si un atributo es heredado (o sintetizado) debe ser siempre heredado (o sintetizado) en todas las producciones.
Si en una regla se le asigna un valor a un atributo heredado de un símbolo, en todas las demás reglas en las que aparezca ese símbolo en la parte derecha se le debe asignar un valor a ese atributo.
Los atributos de los terminales (tokens) son siempre sintetizados y vienen suministrados por el analizador léxico. Los atributos heredados suelen ser “herramientas para la comunicación” entre diferentes partes del árbol.
Sirven a menudo para expresar la dependencia, con respecto al contexto en el que aparece, de una construcción de un lenguaje de programación.

C O M P I L A D O R E S A N T E C E D E N T E S |
- En 1946 nacía Wilo y
El primer ordenador digital.! - Lenguaje máquina
- Lenguaje ensamblador
- En 1950.., John Backus dirigió una investigación en I.B.M. en un lenguaje algebraico.
En 1954 nace FORTRAN (FORmulae TRANslator).
Fue el primer lenguaje considerado de alto nivel, que permitía escribir fórmulas matemáticas de manera traducible por un ordenador.En 1957..
Nace el concepto de un traductor, como un programa que traducía un lenguaje a otro lenguaje. Se introdujo para el uso de la computadora IBM modelo 704.Permitía una programación más cómoda y breve que la existente hasta ese momento, lo que suponía un considerable ahorro de trabajo.
En el caso particular de que el lenguaje a traducir es un lenguaje de alto nivel y el lenguaje traducido de bajo nivel, se emplea el término compilador.
- La tarea de realizar un compilador no fue fácil. El primer compilador de FORTRAN tardó 18 años-persona en realizarse y era muy sencillo.
- Este desarrollo del FORTRAN estaba muy influenciado por una máquina objeto en la que iba a ser implementado. Como Ejemplo de ello tenemos el hecho de que los espacios en blanco fuesen ignorados, debido a que el periférico que se utilizaba como entrada de programas (una lectora de tarjetas perforadas) no contaba correctamente los espacios en blanco.
- Paralelamente al desarrollo del FORTRAN en América, en Europa surgió una corriente más universitaria, que pretendía que la definición de un lenguaje fuese independiente de la máquina y en donde los algoritmos se pudieran expresar de forma más simple.
- Esta corriente estuvo muy influida por los trabajos sobre gramática de contexto libre publicados por Chomsky dentro de su estudio de lenguajes naturales.
- Con estas ideas surgió un grupo europeo encabezado por el profesor F.L.Bauer (de la Universidad de Munich).
Este grupo definió un lenguaje de usos múltiples independiente de una realización concreta sobre una máquina.Pidieron colaboración a la asociación americana A.C.M. (Association for Computing Machinery) y se formó un comité en el que participó J. Backus que colaboraba en esta investigación.
De esa unión surgió un informe definiendo un Internacional Algebraic Language (I. A. L.), publicado en Zurcí (En 1958)
Posteriormente este lenguaje fue revisado y llevó a una nueva versión que se llamó ALGOL 60.
La versión fue ALGOL 68, un lenguaje modular estructurado en bloques. - En el ALGOL
aparecen por primera vez muchos de los conceptos de los lenguajes algorítmicos:- Definición de la sintaxis en notación BNF (Backus-Naur Form).
- Formato libre.
- Declaración explícita de tipo para todos los identificadores.
- Estructuras iterativas más generales.
- Recursividad.
- Paso de parámetros por valor y por nombre.
- Estructura de bloques, lo que determina la visibilidad de los identificadores.
- Junto a este desarrollo en los lenguajes, también se iba avanzando en la técnica de compilación.
En 1958, Strong y otros proponían una solución al problema de que un compilador fuera utilizable por varias máquinas objeto.
Para ello, se dividía por primera vez el compilador en dos fases, designadas como el “front end “y el “back end “. - La primera fase (front end) es la encargada de analizar el programa fuente y la segunda fase (back end) es la encargada de generar código para la máquina objeto.
- El puente de unión entre las dos fases era un lenguaje intermedio que se designó con el nombre de UNCOL (UNiversal Computer Language).
- Para que un compilador fuera utilizable por varias máquinas bastaba únicamente modificar su back end.
Aunque se hicieron varios intentos para definir el UNCOL, el proyecto se ha quedado simplemente en un ejército teórico.
De todas formas, la división de un compilador en front end y back end fue un adelanto importante. - En 1959.. se van poniendo las bases para la división de tareas en un compilador.
En 1959 Rabin y Scout proponen el empleo de Autómatas Deterministas y No Deterministas para el reconocimiento lexicográfico de los lenguajes.Rápidamente se aprecia que la construcción de analizadores léxicos a partir de expresiones regulares es muy útil en la implementación de los compiladores.
En 1968, Johnson apunta a diversas soluciones.
En 1975, con la aparición de LEX surge el concepto de un generador automático de analizadores léxicos a partir de expresiones regulares, basado en el sistema operativo UNIX. - A partir de los trabajos de Chomsky ya citados, se produce una sistematización de la sintaxis de los lenguajes de programación, y con ello un desarrollo de diversos métodos de análisis sintáctico.
- Con la aparición de la notación BNF – desarrollada en primer lugar por Backus en 1960 cuando trabajaba en un borrador del ALGOL 60, modificada en 1963 por Naur y formalizada por Knuth en 1964 – se tiene una guía para el desarrollo del análisis sintáctico.
- Los diversos métodos de parsers ascendentes y descendentes se desarrollaban durante la década de los 60.
- En 1959, Sheridan describe un método de parking de FORTRAN que introducía paréntesis adicionales alrededor de los operandos para ser capaz de analizar las expresiones.
Más adelante, Floyd introduce la técnica de la precedencia de operador y el uso de las funciones de precedencia.
A mitad de la década de los 60, Knuth define las gramáticas LR y describe la construcción de una tabla canónica de parser LR. - Por otra parte, el uso por primera vez de un parking descendente recursivo tuvo lugar en el año 1961. En el año 1968 se estudian y definen las gramáticas LL así como los parsers predictivos.
También se estudiaba la eliminación de la recursión a la izquierda de producciones que contienen acciones semánticas sin afectar a los valores de los atributos. - En la década de los 70, se describen los métodos SLR y LALR de parser LR.
Debido a su sencillez y a su capacidad de análisis para una gran variedad de lenguajes, la técnica de parking LR va a ser la elegida para los generadores automáticos de parsers.
A mediados de los 70, Johnson crea el generador de analizadores sintácticos YACC para funcionar bajo un entorno UNIX. - Junto al análisis sintáctico, también se fue desarrollando el análisis semántico.
En los primeros lenguajes (FORTRAN y ALGOL 60) los tipos posibles de los datos eran muy simples, y la comprobación de tipos era muy sencilla.
No se permitía la coerción de tipos, pues ésta era una cuestión difícil y era más fácil no permitirlo. - Con la aparición del ALGOL 68 se permitía que las expresiones de tipo fueran construidas sistemáticamente.
Más tarde, de ahí surgió la equivalencia de tipos por nombre y estructural. - El manejo de la memoria como una implementación tipo pila se usó por primera vez en 1958 en el primer proyecto de LISP.
La inclusión en el ALGOL 60 de procedimientos recursivos potenció el uso de la pila como una forma cómoda de manejo de la memoria.
Dijkstra introdujo posteriormente el uso del display para acceso a variables no locales en un lenguaje de bloques. - También se desarrollaron estrategias para mejorar las rutinas de entrada y de salida de un procedimiento.
Así mismo, y ya desde los años 60, se estudió el paso de parámetros a un procedimiento por nombre, valor y variable. - Con la aparición de lenguajes que permitan la localización dinámica de datos, se desarrolla otra forma de manejo de la memoria, conocida por el nombre de heap (montículo).
Se han desarrollado varias técnicas para el manejo del heap y los problemas que con él se presentan, como son las referencias perdidas y la recogida de la basura. - La técnica de la optimización apareció desde el desarrollo del primer compilador de FORTRAN.
Backus comenta cómo durante el desarrollo del FORTRAN se tenía el miedo de que el programa resultante de la compilación fuera más lento que si hubiera escrito a mano.
Para evitar esto, se introdujeron algunas optimizaciones en el cálculo de los índices dentro de un bucle. - Pronto se sistematizan y se recoge la división de optimizaciones independientes de la máquina y dependientes de la máquina.
Entre las primeras están la propagación de valores, el arreglo de expresiones, la eliminación de redundancias, etc.
Entre las segundas se podría encontrar la localización de registros, el uso de instrucciones propias de la máquina y el reordenamiento de código. - A parir de 1970 comienza el estudio sistemático de las técnicas del análisis de flujo de datos.
Su repercusión ha sido enorme en las técnicas de optimización global de un programa. - En la actualidad, el proceso de la compilación ya está muy asentado.
Un compilador es una herramienta bien conocida, dividida en diversas fases.
Algunas de estas fases se pueden generar automáticamente (analizador léxico y sintáctico) y otras requieren una mayor atención por parte del escritor de compiladores ( las partes de traducción y generación de código ). - De todas formas, y en contra de lo que quizá pueda pensarse, todavía se están llevando a cabo varias vías de investigación en este fascinante campo de la compilación.
Por una parte, están mejorando las diversas herramientas disponibles (por Ejemplo, el generador de analizadores léxicos Aadvard para el lenguaje PASCAL).También la aparición de nuevas generaciones de lenguajes – ya se habla de la quinta generación, como de un lenguaje cercano al de los humanos – ha provocado la revisión y optimización de cada una de las fases del compilador.
- El último lenguaje de programación de amplia aceptación que se ha diseñado, el lenguaje Java, establece que el compilador no genera código para una máquina determinada sino para una virtual, la Java Virtual Machine ( JVM ), que posteriormente será ejecutado por un intérprete, normalmente incluido en un navegador de Internet.
El gran objetivo de esta exigencia es conseguir la máxima portabilidad de los programas escritos y compilados en Java, pues es únicamente la segunda fase del proceso la que depende de la máquina concreta en la que se ejecuta el intérprete.
Aquella máquina realizaba instrucciones
- Registradas en códigos numéricos
- De circuitos de la máquina
- Y estados de cada operación.
Códigos numéricos, interpretado por un secuenciador cableado o por un microprograma.
Los códigos numéricos se traducían manualmente a Lenguaje Máquina.
Tales claves, se generalizaron al hacer que las propias máquinas realizaran el proceso de traducción.
Esta operación se le llama ensamblar el programa.
y su sabiduría, por lo que dice.
Taleb

para definir LENGUAJES DE PROGRAMACIÓN |
- CARACTERÍSTICAS de tu PROBLEMA
- En la WEB:
Se impone que uses JAVA , HTML y PHP - De BASES DE DATOS
Inicia con con VISUAL FOX y luego profundizar con SQL.
Puedes operar bases de datos con Visual Basic o Delphi, pero estos, como C++ Builder usan instrumentos intermediarios, tales como los tipo record set, que generan sistemas "más pesados" que insumen más recursos de tu configuración. - Soft de APLICACIÓN:
Usa lenguaje C o C++ - Soft ENLATADO:
Usa los entornos
- C++ Builder o
- DELPHI
- Visual Studio Net. - LOS DATOS
- DATO SIMPLE
- NUMERICO
- Entero
- Real
- Decimal
- Exponencial
- NO NUMERICO
- Boleano
- Caracter
- DATO ESTRUCTURADO
- ESTATICO
- Arreglo
- Enunciado
- Cadena
- Registro
- Conjunto
- DINAMICO
- ARCHIVO
- PUNTERO
- Lineal
- Cola
- Pila
- Lista
- No Lineal
- Arbol
- Lineal
- TIPOS DE PROGRAMACION
- PROGRAMACION BASADO EN REGLAS:
De aplicación en la ingeniería del conocimiento para desarrollar sistemas expertos, con núcleo de reglas de producción del tipo if then. - PROGRAMACIÓN LÓGICA:
Entorno de programación conversacional, deductivo, simbólico y no determinista apoyada en asertos y reglas lógicas. - PROGRAMACIÓN FUNCIONAL:
Entorno de programación interpretativo, funcional y aplicativo, de formato funcional. - PROGRAMACIÓN HEURÍSTICA:
Moldean los problemas para aplicar heurísticas según sistemas de visualización, búsqueda y métodos de solución. Pueden ser:4.1.-Programación Paralela
4.2.-Programación Orientado a Objetos
4.3.-Programación Basado en Restricciones
4.4.-Programación Basado en Flujo de Datos
- CONFIGURACION de tu EQUIPO
Un lenguaje es más apropiado que otro, según el tipo de información a procesar.
Si tu problema requiere efectuar transacciones:
No olvides que la mejor regla te aconseja:
En administración, ademas de la eficiencia, esto mejora la rentabilidad de tu sistema..!!
La elección de un lenguaje adecuado, también pasa por conocer la clase de información de tus transacciones
En el mundo algorítmico, los datos debemos entenderlos como la información
que deseamos procesar con nuestros programas.
Que podemos organizarlos así:
Otro factor más que determinante para que adoptes un lenguaje para que desarrolles tus sistemas es la "Escuela de Programación" de tu corazoncito, que dominas y que por tanto, te resulta familiar.
De acuerdo a este criterio, por Ejemplo, si no dominas la filosofía de la programación orientada a objetos, no podrás optar por el poderoso lenguaje Java.
En esta introducción solo te enumero las alternativas mas tradicionales. Más adelante, en mis links te desarrollo la teoría paradigmática correspondiente y encontrarás una descripción más detallada.
Juega un factor determinante el software de desarrollo con que cuentes y por tanto el hardware que poseas para operar el lenguaje que hayas elegido. Recuerda que trabajo creativo será menos tedioso si tienes frente tuyo "La maquina capaz de procesar el soft de ultima generación".
Te recomiendo verificar, además del correcto funcionamiento tanto en la edición como en la compilación y la depuración de tus programas; el aspecto legal, especialmente del software de desarrollo. Conviene que seas un combatiente del software apócrifo e ilegal.
Guiado por estos criterios, en función de las características particulares de tu problema, y de la configuración del equipo que dispones, ahora ya puedes adoptar el lenguaje de programación que más se adecua a tus necesidades particulares.
Olvida que eres indispensable
en tu trabajo, tu casa o tu grupo habitual.
Por más que eso te desagrade,
todo camina sin tu actuación,
salvo vos mismo..!!
(Wilucha)
|
ANTECEDENTES |
- Evoluciòn en el tiempo:
- Edad media:
- Nacen diccionarios y gramáticas.
- Traducen antiguos textos. - Elio de Nebrija: Escribe
- Gramática de lengua española. - Cardenal Cisneros: Escribe
- Biblia Políglota Complutense. - Francisco Sánchez: Escribe
Minerva. Abarca:
- Partes gramáticales
- Categorías léxicas.
- Normas de uso del idioma. - Racionalismo, rechaza:
- Origen comun de especie humana
- y de una sola lengua. - Alexander von Humboldt: Escribe
Teoría general del lenguaje
- El lenguaje es energía.
- Distingue lo fónica y conceptual. - Discípulos de Saussure,
Bally y Séchehaye, publican:
"Curso de Lingüística General",
Nace la Ciencia del lenguaje
- Edad media:
- ESTUDIO APLICADO:
Lenguaje como medio aplicado:
- Enseñanza de idiomas.
- Terapia de trastornos de lenguaje.
- Traducción automática.
- Reconocimiento de la voz.- ESTUDIO SINCRONICO:
La lengua en un periodo de tiempo.- ESTUDIO DIACRONICO:
Evolución del lenguaje en el tiempo.- LINGÜISTICA COMPARADA:
Compara conceptos universales.
- Clases, métodos y criterios.
- Formas sintácticas y Gramáticales,- PSICOLINGÜISTICA:
Estudia:
- Proceso para adquirir una lengua.
- Trastornos como la disfasia.
- Mecanismos neurolingüísticos
- Relaciones Cerebro-Lenguaje.- SOCIOLINGÜISTICA:
Lenguaje en la sociedad. Ejemplo:
Cómo dirigirse al interlocutor:
- Señor, señora, ingeniero, doctor
Mucha de la información que hallarás en mis pages
podras ampliarlos en:
BIBLIOGRAFÍA
LIBRO AUTOR EDITORIAL
Teoría de autómatas - Hopcroft, Motwani - Adison Wesley
Teoría de autómatas lenguajes - Hopcroft, John E. Jeffrey - CECSA, México
Autómatas y Lenguajes Formales - DEAN KELLEY - Prentice Hall
Lenguajes, Gramáticas y Autómatas - Pedro ISASI Martinez Borrajo - Adison Wesley
Teoría de la Computación - J. G. Brookshear - Addison-Wesley
Lenguajes,Gramáticas y Autómatas - Alfonseca, Sancho Martínez - Ediciones Unive
eBook: Teoría de Autómatas - G. Morales - CINVESTAV-IPN
Visual C#.NET - Cristina Sanchez - Edit MACRO
Visual C# - Erika Alarcon - Megabyte
Programación C++ - Luis Joyanes - Mc Graw Hill
C++ Cómo programar - Deitel y Deitel - Prentice Hall
Visual C++ - Kate gregory - Prentice Hall
Visual C++ - Cris H. Pappas - Mc Graw - Hill
Visual C++ Manual - Beck Zaratian - Mc Graw Hill
Visual C++ - Holzner - Mc Graw Hill
Manual C / C++ - Wiliam H. Murray - Mc Graw Hill
Visual C++ - María Cascon Sánchez - Prentice Hall
Visual C++ - Ori y Nathan Gurenwich - SAMS Publishing
C++ Builder - Fransisco Charte - Anaya
Visual FoxPro Manual - Microsoft Corporation - Mc Graw Hill
Visual Fox Pro - Pedro Hernandez Muñoz - Mc Graw Hill
Delphi - Germán Galeano Gil - Anaya
Delphi - Kent Reisdorph - Prentice Hall
Delphi - Tom Swan - Anaya
Java J++ - Stephen R Davis - Mc Graw Hill
Visual J++ - Microsoft Press
Visual Basic - Javier Ceballos - RAMA
Visual Basic - Microsoft Press
Visual Basic - William R. Vaughn - Mc Graw Hill
Orientación a Objetos - Carlos Fontela - Nueva Librería
Cultivo una rosa blanca
..en julio, como en enero
para el amigo sincero
que me da su mano franca..!!
Y para el cruel que me arranca
el corazón con que vivo,
cardo ni ortiga cultivo;
..cultivo una rosa blanca..!
José Martí

Esta page está en: Te espero en: 20/11/2014
www.wilocarpio.com
wilocarpio@gmail.com


 LENGUAJES NATURALES
LENGUAJES NATURALES LENGUAJES ARTIFICIALES
LENGUAJES ARTIFICIALES


